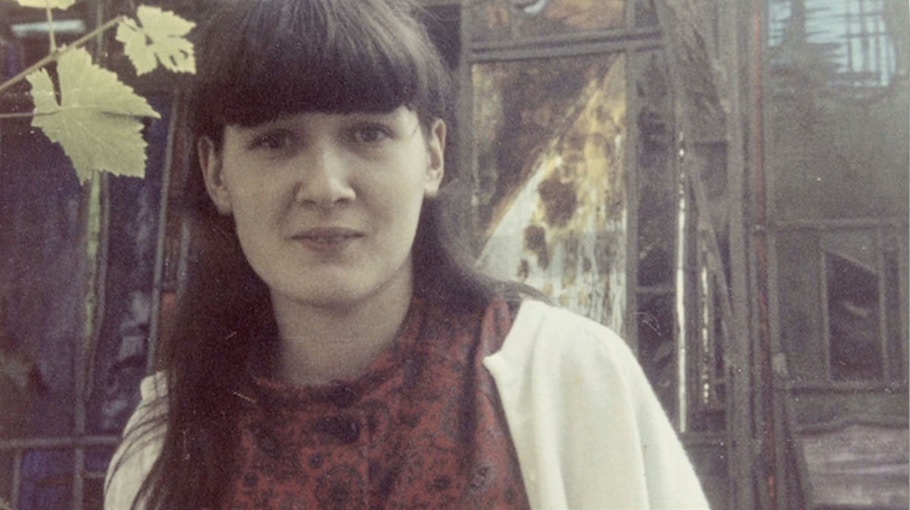Dusa McDuff
- Highlights (2:14)
- Childhood (2:34)
- Ancestry (3:27)
- Becoming Rebellious (3:17)
- Early Interest in Mathematics and Music (4:18)
- Parental Support in Choosing Mathematics (3:17)
- Studying with Gelfand in Russia (4:30)
- Maturing as a Mathematician (2:51)
- Being a Female Mathematician (3:20)
- Moving Toward Symplectic Geometry (3:56)
- Going to Stony Brook (2:08)
- Symplectic Topology (3:00)
- Collaboration with Dietmar Salamon (1:47)
- Toric Geometry (2:26)
- Favorite Theorem (2:17)
- Evolution of Geometry (3:13)
- Convergence of Ideas on Symplectic Geometry (4:05)
- Christopher Zeeman and Warwick Institute (3:27)
- Learning to Cope (2:17)
- Mathematics in the UK (1:33)
- Challenges for Women in Mathematics (6:53)
- Origin of Name Dusa (1:54)
- Boys and Girls Are the Same (1:54)
- Importance of Symplectic Geometry (2:44)
- Is Mathematics Discovered or Invented (9:26)
- Children's Games and Mathematics (3:55)
- The Future of Sympletic Topolog (2:37)
- MSRI (4:38)
A trip to Moscow in 1969 was a turning point for Dusa McDuff, then a promising young mathematician who was yet to find her mathematical path. In Soviet-era Moscow, many would-be artists or writers had instead become mathematicians. The creativity they brought to mathematics was a revelation to McDuff, who had just finished her second year as a graduate student at Cambridge University. She had already produced a solution to a well-known problem about von Neumann algebras that had been published in the Annals of Mathematics, gaining her some attention in mathematics circles. But in 1969 she was in Moscow because her then-husband was researching the poetry of Innokenty Annensky, and she had given little thought to what the trip would contribute to her education and future career. At the student office at Moscow State University, she was hardly prepared when asked to name someone she’d like to work with, and she gave the first name that came to mind: I. M. Gelfand. By chance, she had read his work as an undergraduate.
Gelfand, legendary for his broad interests and wide-ranging seminar series, became an important mentor during the six months she spent in Moscow. He spoke of mathematics not in terms of beautiful theorems and abstract constructions but as a part of the larger world, connected to everything. He and McDuff discussed all kinds of mathematical ideas, considering how they emerged and were related to each other, while also analyzing Pushkin’s writings and Bach’s music. McDuff remembers realizing the narrowness of her own mathematical education. It was during this period that she was introduced to topology, which concerns the properties of shapes and spaces, a subject she continued to study upon returning to Cambridge. This led to collaborations, mostly via letters, with the British mathematician Graeme Segal, who was at Oxford. By the early 1980s she found herself working in the emerging field of symplectic geometry. She went on to dedicate the rest of her career to symplectic geometry, making significant contributions to a field that has grown into one of the most active branches of mathematics.
+++

“People often show up at my office huffing and puffing,” says McDuff. Her office is at the end of a corridor on the sixth floor of the mathematics building at Columbia University. Since 2007, McDuff has been the Helen Lyttle Kimmel ’42 Professor of Mathematics at Barnard College. Visitors are rewarded with walls covered with vibrant art — paintings by abstract expressionists such as Miró, Matisse and Kandinsky. “I don’t go in for minimalism,” she says. “I like color, I like the interaction of interesting shapes.”
McDuff spends a lot of time thinking about shapes, though the ones that preoccupy her are stranger than the ones depicted on her walls and much more difficult to visualize. Symplectic geometry — “sym” comes from the Greek for “together with” — is a branch of geometry that concerns shapes in even-numbered dimensions. Like the Euclidean geometry that everyone learns in school, symplectic geometry concerns the study of space, but this branch of geometry also considers the additional dimensions of time and movement.
Barnard College needed senior faculty to teach undergraduate math classes, so McDuff volunteered and for the last few years has been teaching an introductory calculus course in addition to advanced courses in topology and geometry. “I wouldn’t do it if I didn’t enjoy it,” she says. She tries to show her calculus students that the math they learn in class has real meaning in the world. “Because they’re not math majors, I try to teach it as a practical subject.”
Symplectic geometry, although seemingly less practical and more esoteric than calculus, nevertheless has roots in classical mechanics. In the early 1800s, the first symplectic manifolds were conceptualized to describe the motion of the planets under the influence of their gravitational interaction. In that sense, symplectic geometry picked up where Newton’s calculus left off as a means of understanding dynamic systems. Today it is used to describe how space probes move in different gravitational fields or how charged particles move in an accelerator. Mathematical physicists like Edward Witten, who studies string theory at the Institute for Advanced Study in Princeton, N.J., have made many predictions in symplectic geometry that converge with new ideas in theoretical physics.
+++
McDuff was born in London in 1945 but was raised in Edinburgh, Scotland. Her father, Conrad Hal Waddington, was a distinguished geneticist, developmental biologist and philosopher who for a time was the director of the Institute of Animal Genetics at the University of Edinburgh. Housing was tight during World War II, so her father moved the family, along with everyone in his lab and their families, into Mortonhall, a large stone mansion outside Edinburgh. This experiment in communal living, where families shared rations and took turns cooking, proved challenging for the adults, but quite wonderful for the children, McDuff remembers.
McDuff and her sister, Caroline (now a professor of social anthropology at Cambridge), were encouraged to excel academically and grew up with the expectation that they would have careers. McDuff descends from a notable line of female intellectuals. Her great-grandmother was the feminist writer Maud Pember Reeves, who helped New Zealand become the first country in the world to grant the vote to women; McDuff’s grandmother, Amber Reeves, was also a politically minded writer who had a much-publicized affair with H. G. Wells; and McDuff’s mother was an architect who worked for the Scottish civil service.
Yet even in such a progressive family, women were not on an equal footing with men. “I grew up in a house in which creativity was very much valued but, despite the achievements of the women in the family, males were seen to be more truly creative than females, and it has taken me a long time to find my own creative voice,” McDuff recalled many years later upon accepting the inaugural Ruth Lyttle Satter Prize, which recognizes outstanding contributions to mathematics research by women.
Her earliest mathematical memory is of being shown a 10-by-10 multiplication table by her maternal grandfather at the age of four. Even at that early age she was impressed and delighted by the table’s repeating symmetries and patterns. She was a precocious student and showed a propensity for both music and mathematics, the latter helped along by a good math teacher in high school. She ultimately chose to study mathematics in college, but she is still an avid cello player. As a teenager she befriended “genius-type young men,” she says, but had few female friends — she found that other girls did not share her ambition. “I always thought I would have a career — my parents brought me up to want a career. But I didn’t know how to get a career.”
(Courtesy of Dusa McDuff)
She passed over an undergraduate scholarship to Cambridge and enrolled at the University of Edinburgh because her first husband, David McDuff, was a student there. She went on to graduate studies at Cambridge, earning her doctorate in 1971, and stayed two years as a postdoc. Because there were few women and no accommodations for married students, she felt separate from the mathematical community at Cambridge and worked largely in isolation.
Although her time in Moscow during her graduate studies had given her a glimpse of wider mathematical horizons, it also set up the challenge of switching mathematical directions, away from functional analysis and toward topology. McDuff remembers these transitional years after her return from Moscow as the hardest of her career. She read up on her new field intensively but often felt unsure of her ability to do original research. Meanwhile, she was both the breadwinner for her family and the primary caretaker of a young daughter. She did not know any female mathematicians who could serve as role models. Not until the summer of 1972, when she met Segal, whom she credits as a significant mathematical influence, did she feel she “had some context in which to work.” That year, with only four open lectureships in math in all of Britain, she won a teaching position at the University of York.
In 1974, McDuff took another pivotal journey, this time to the Massachusetts Institute of Technology as a visiting assistant professor. There, for the first time, she met other female mathematicians to whom she could relate. She realized she could be more proactive about her own career. She applied for a visiting position at the Institute for Advanced Study, then to a job at the University of Warwick, and received both. While at MIT, she published a paper with Segal on the group-completion theorem.
In 1978, McDuff moved to the State University of New York at Stony Brook. Her work became more focused on symplectic geometry just as the field was taking off. “I was never good at picking problems,” she says. “I came to symplectic geometry just as new tools and interesting questions opened up in the mid-’80s. I just happened to start working in that area. So it was really chance.” But she has undeniably played a central role in advancing the field, contributing many fundamental theorems as well as an extension to Mikhail Gromov’s non-squeezing theorem. She is a fellow of the Royal Society of London, a member of the National Academy of Sciences, a fellow of the American Mathematical Society, and a member of the American Philosophical Society.
+++
“I would describe Dusa McDuff as a very dynamic person with an amazing energy, broad interests, very wide knowledge, many original ideas, and deep insights,” says Dietmar Salamon, a professor of mathematics at ETH Zurich, who has collaborated with McDuff since 1990 when she attended a symplectic geometry conference at the University of Warwick that Salamon organized. “At the time we had both given lecture courses on symplectic topology and were writing lecture notes for them, and decided to put our acts together to write a joint book.” They have since written three books together, including “Introduction to Symplectic Topology” in 1995, the first comprehensive introductory text on the subject.
“To work with her was and is certainly inspiring, and our interaction has been very fruitful,” says Salamon. “We are of course both opinionated on occasion, but have learned to compromise in the course of our joint work, with an outcome that’s much better than if one of us had written it alone.”
+++
In her office at Columbia, McDuff points out a few favorite artworks on her wall: a painting by Joan Mitchell, one of the few prominent female artists of the abstract expressionist movement, and a series of landscapes by Emily Carr, an early 20th-century Canadian painter who depicted the indigenous cultures of the Pacific Northwest and worked for many years in relative isolation and obscurity. Women painters were long excluded from the mainstream, McDuff says with fellow feeling.
The challenges of McDuff’s early career have helped her become the mathematician she is today. Once doubtful of her mathematical creativity, she has found a confident voice. “What I find appealing about mathematics is the power of your ideas,” she says. “Math is amazing because you can look at two completely different problems and see a similar structure in very unrelated areas.” She compares the daily work of a research mathematician to that of a playwright — both are creating new worlds in their own way.
Once isolated in a male-dominated field, McDuff is now a frequent collaborator with mathematicians around the world and a passionate advocate for the next generation of women in mathematics. “In the 1980s I realized I needed more support and became interested in the lives of women,” she says, adding that even today some people will say the reason for the small number of female mathematicians is that women lack talent. She counters those biases by mentoring students at Barnard and the Institute for Advanced Study and, just as essentially, by continuing her work as a mathematical researcher.
“My life as a young mathematician was much harder than it needed to be because I was so isolated,” McDuff said in her acceptance speech for the Satter Prize in 1991. “One important way of combating such isolation is to make both the achievements of woman mathematicians and the different ways in which we live more visible.”