MPS Awardee Spotlight: Randall Kamien

Randall Kamien is a 2013 Simons Investigator in Physics and the Vicki and William Abrams Professor in the Natural Sciences in the Department of Physics and Astronomy at the University of Pennsylvania. He received both his B.S. and M.S. from the California Institute of Technology and his Ph.D. from Harvard University. Kamien conducts research on problems in soft condensed matter theory and incorporates kirigami, a Japanese paper-folding technique that allows cuts as well as folds, into aspects of his work.

Kamien has found that many problems in soft condensed matter theory can be formulated very naturally as geometry or topology problems. “We look at problems where often the solution is about drawing a picture or building a tinker toy model of what we’re trying to understand,” explains Kamien. “And then we have to understand why the tinker toy model is the right answer. In this way, we try to find rigorous results that we can apply to solve our problems.”

Kamien is especially fond of working with liquid crystals: the kind used in many types of consumer electronics displays. A great variety of liquid crystals are now being made in laboratories around the world, and these, Kamien observes, provide an important opportunity to study the connections between geometry, topology and material properties. “You can think about how defects in the materials move and interact and wonder, could you reconstruct the entire texture of the liquid crystals just by looking at the defects in the material?”

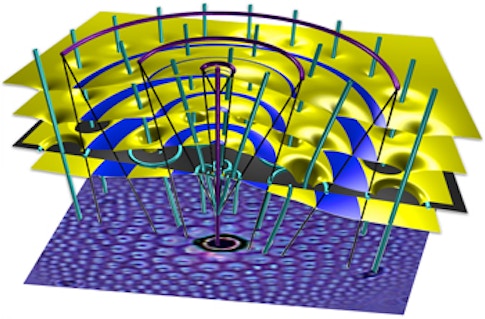
Kamien and his group have been looking at different phases of liquid crystals that might appear to be mathematically similar, but can be differentiated based on the types of defects they can support. “It turns out they are completely different. Even though you would think that the space of ground states are the same in these systems, there’s something hidden in in their mathematical description that further separates the materials.”

On his way to the Simons Foundation offices in New York City, Kamien noted that the walkways in Madison Square Park were made with hexagonal tiles. “I at first wondered how they could make the borders on the edges so nice — but they can’t! All the mistakes are on the borders. They could instead make the borders nice and resolve everything in the middle. These things happen with liquid crystals, and they happen in other materials: it’s boundary conditions.”
 

• Toen Castle, Yigil Cho, Xingting Gong, Euiyeon Jung, Daniel M. Sussman, Shu Yang, and Randall D. Kamien, “Making the Cut: Lattice Kirigami Rules,” Phys. Rev. Lett. 113, 245502 (December 2014)
• Daniel A. Beller, Mohamed A. Gharbi, Apiradee Honglawan, Kathleen J. Stebe, Shu Yang, and Randall D. Kamien, “Focal Conic Flower Textures at Curved Interfaces,” Phys. Rev. X 3, 041026 (December 2013)