The Ups and Downs of Modeling Oscillation

Fruzsina Agocs started her career as a theoretical cosmologist. But she quickly found that there weren’t enough mathematical and computational tools for running the models she wanted to use. As she delved into the mathematics to make the tools she needed, Agocs discovered she enjoyed the methodology. That led her down a path to focus solely on making better tools for other scientists to use in their own models.

Today, Agocs is a Research Fellow at the Flatiron Institute’s Center for Computational Mathematics (CCM), where she works with the Numerical Analysis group. Prior to that, she earned her doctorate in theoretical and computational cosmology, as well as a master’s and a bachelor’s degree in physics, from the University of Cambridge.

Agocs spoke with the Simons Foundation about her work and the surprising acoustics of staircases. The conversation has been edited for clarity.

What projects are you working on right now?

I study oscillating systems. These are systems that have some kind of back-and-forth or up-and-down, repeating motion. A very simple example would be a teeter-totter. However, most oscillating systems are far more complex; equations describing them cannot be solved by humans using paper and pen. Even computers struggle to solve these equations, taking a long time to work out an approximate solution.

I am working on designing and implementing methods to make it easier for computers to solve these equations, and to do so efficiently and accurately. One of the projects is developing numerical methods to enable the evaluation of cosmological models. Very early in the universe’s history — the very first moments after the Big Bang ­— there were oscillations in the density of matter. I’m working on ways to figure out what kinds of particles the matter was made of, and how that matter interacted with other particles and itself. I’m also interested in the curvature of spacetime at that critical juncture — essentially what was the geometry of the universe. That curvature is important because it can tell us a lot about the overall evolution — and ultimate fate — of the universe.

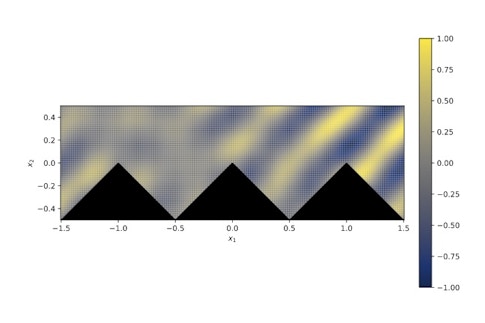
I recently started another project, which is based in acoustics. I’m looking at the scattering of sound waves off specific surfaces called quasi-periodic surfaces. An example of this type of surface is an infinitely tall staircase. Obviously, these don’t exist in real life, but there are some very long staircases out there, such as ancient, stepped temples like Mesopotamian ziggurats, Mayan temples, and Greek theaters. These have really long staircases that exhibit interesting acoustic phenomena. For example, sound travels up along the stairs extremely well, and if you clap near them, reflected sound can sound like a chirp or raindrops instead of a clap. I want to reproduce these acoustic phenomena numerically because with computers we finally have the tools to do this with high accuracy. Ultimately, understanding how these surfaces reflect sound can help guide the design of buildings such as auditoriums.

Why is it so difficult to analyze these surfaces?

A staircase is mathematically interesting because it poses some unique challenges, namely that the point where two stairs meet — the corner — is described in mathematics as a singularity. This means when you’re writing down a formula to describe this point, you would get an infinite value, which is impossible for a computer to handle. When you solve this problem numerically, you have to be very careful as you approach the singularity in order to not lose accuracy.

Another challenge arises from the infinite length of the staircase, since naively this would result in an infinitely long runtime of any computer code. To overcome this, one has to exploit the repeating pattern of the structure — its symmetry — to reduce the problem to a single repeating unit of the staircase. With this mathematical trick, it actually becomes simpler to solve for an infinite staircase than a really long, finite one.

How do you go about simulating these systems?

Day-to-day I do a lot of pen-and-paper analytic work. I derive relevant equations to see if I can take any shortcuts or find any simplifications that I could use in my model. I also work on algorithm design, which is essentially working at a blackboard to make a blueprint for my code, figuring out how I want it to work and what parameters I will need. And then of course there’s actually writing code. But the majority of my work is on a piece of paper. There’s a lot of numerical analysis that goes into every line of code I write.

Do you hope other people will use your code?

Yes, I put an emphasis on making tools that are usable by others. When I finish a project, I first release a very detailed description of the method I used and any relevant proofs, in the form of a publication in a scientific journal. This helps people know what limits the method and code have. Then I release the code as open-source software, often in a journal for open-source software that is peer-reviewed.

I’ve also collaborated on various projects with researchers from around the world. For example, I worked with a group of astrophysicists at the University of Göttingen in Germany on a particle physics problem. They were modeling different particles that could be candidates for dark matter but needed help with some of the details in the model. These researchers provided guidance on what models they needed to search for these particles, and I helped improve the accuracy and speed of computational methods needed to run the models.

Ultimately, my goal is to enable scientists to consider models that have previously been too challenging to compute. For this, my methods need to be robust and usable out-of-the-box, so I really pay attention to writing quality code. I think it’s important to prove that your code will actually work, and not just have a few examples that show it works in those specific cases. Collaborating with people here at the CCM allows me to draw on the expertise of others to help rigorously show that the method will work and push the boundaries of high-accuracy numerical computation.