Foundation Announces the Simons Collaboration on Celestial Holography

The Simons Foundation is pleased to announce the Simons Collaboration on Celestial Holography, directed by Andrew Strominger at Harvard University. Information regarding the collaboration’s kickoff meeting can be found here.

The holographic principle originates in the enigmatic quantum physics of black holes and efforts to reconcile quantum mechanics with general relativity. It hypothesizes that any bulk quantum theory of gravity has an equivalent ‘dual’ presentation as a quantum theory of matter without gravity living on the spacetime boundary. A precise realization for negatively-curved spacetimes, constructed top-down from string theory, is provided by the Anti-de Sitter(AdS)/conformal field theory (CFT) correspondence. We seek to realize the holographic principle in (nearly) asymptotically flat spacetimes like the one we inhabit, guided by but not assuming AdS/CFT or string theory. Recent discoveries make this so-far-elusive goal plausibly within reach, using a combined bottom-up and top-down approach which has come to be known as celestial holography.

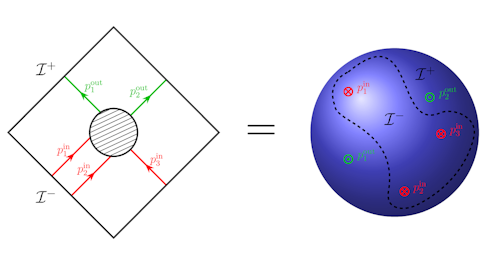
The first (bottom-up) step in the construction of any holographic dual pair is the identification of symmetries which must govern both sides of the pair. Using recent syntheses of old and new results on asymptotic symmetries, soft theorems and gravitational memory, it has been shown that any quantum gravity scattering matrix enjoys the conformal symmetries of a two-dimensional CFT living on the celestial sphere at light-like infinity. This ‘celestial CFT’ provides a potential holographic dual for four-dimensional quantum gravity in asymptotically flat spacetimes. The conformal symmetries are only one entry in an infinite tower of symmetries known as w-infinity which played a central role a half-century ago in Penrose’s solution of twistor theory.

One would also like to have a mathematically rigorous top-down construction of a celestial holographic dual pair. Even if simplified or physically unrealistic, it could usefully guide the bottom-up construction of a hologram for the natural world. Fortuitously, there has been a recent explosion of complementary advances in mathematical physics which leverages techniques from algebraic geometry and homological algebra to define quantum structures on twistor space and compute a broad class of both bulk and boundary observables in a variety of models. These independent efforts landed on precisely the same mathematical structures as those sought in the bottom-up approach. The goal of this project is to exploit this synergy and understand holography in flat spacetimes along with the concomitant mathematics.