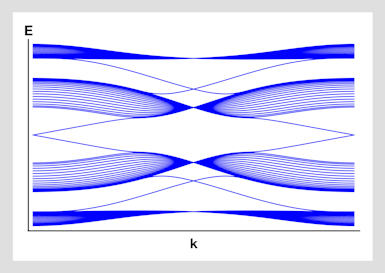
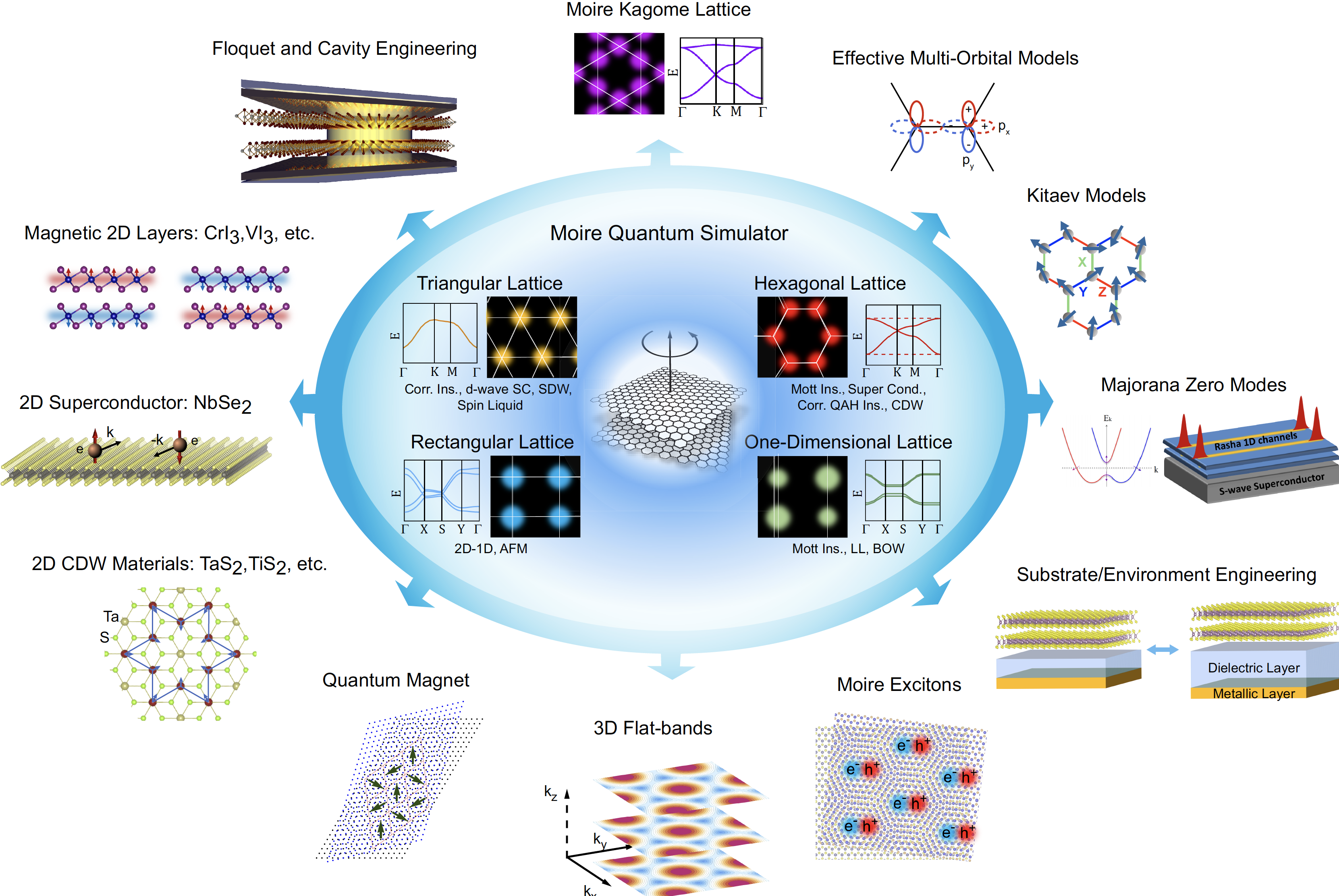
One of the exciting discoveries of recent years is the novel properties of quantum materials including dissipationless surface/edge currents, quantized anomalous Hall effects, unusual symmetry breaking and unconventional superconductivity. At CCQ we are developing and implementing the new tools needed to understand and control these remarkable systems.
Research
- Topological materials
-
- Topological materials have a unique bulk-edge correspondence that is of fundamental scientific interest and may also have practical implications for future technology utilizing dissipationless surface currents. At CCQ we are focused on finding material and synthetic realizations of topological systems, as well as answering fundamental theoretical questions about the types of phases that can exist, the interplay between symmetry and topology, and the effects of interactions.
-
-
- Current projects include ab initio modeling of topological materials, manipulating topological surface states with superlattice potentials, and topological aspects of moire materials.

-
-
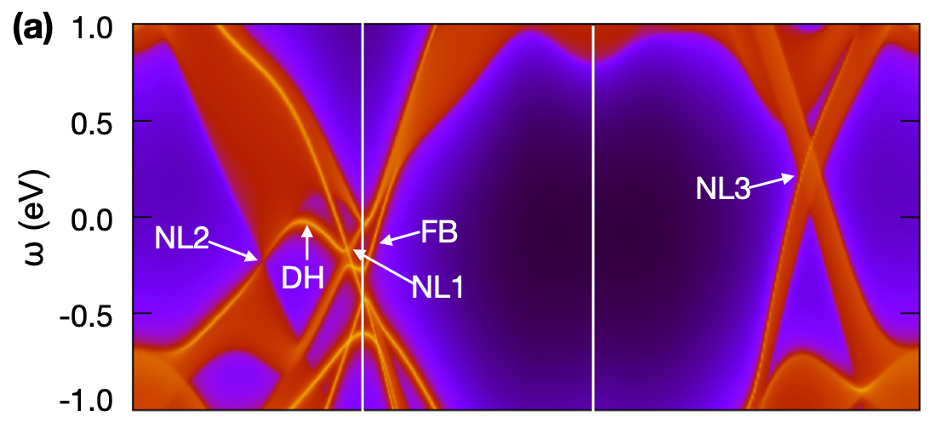
- Moire materials
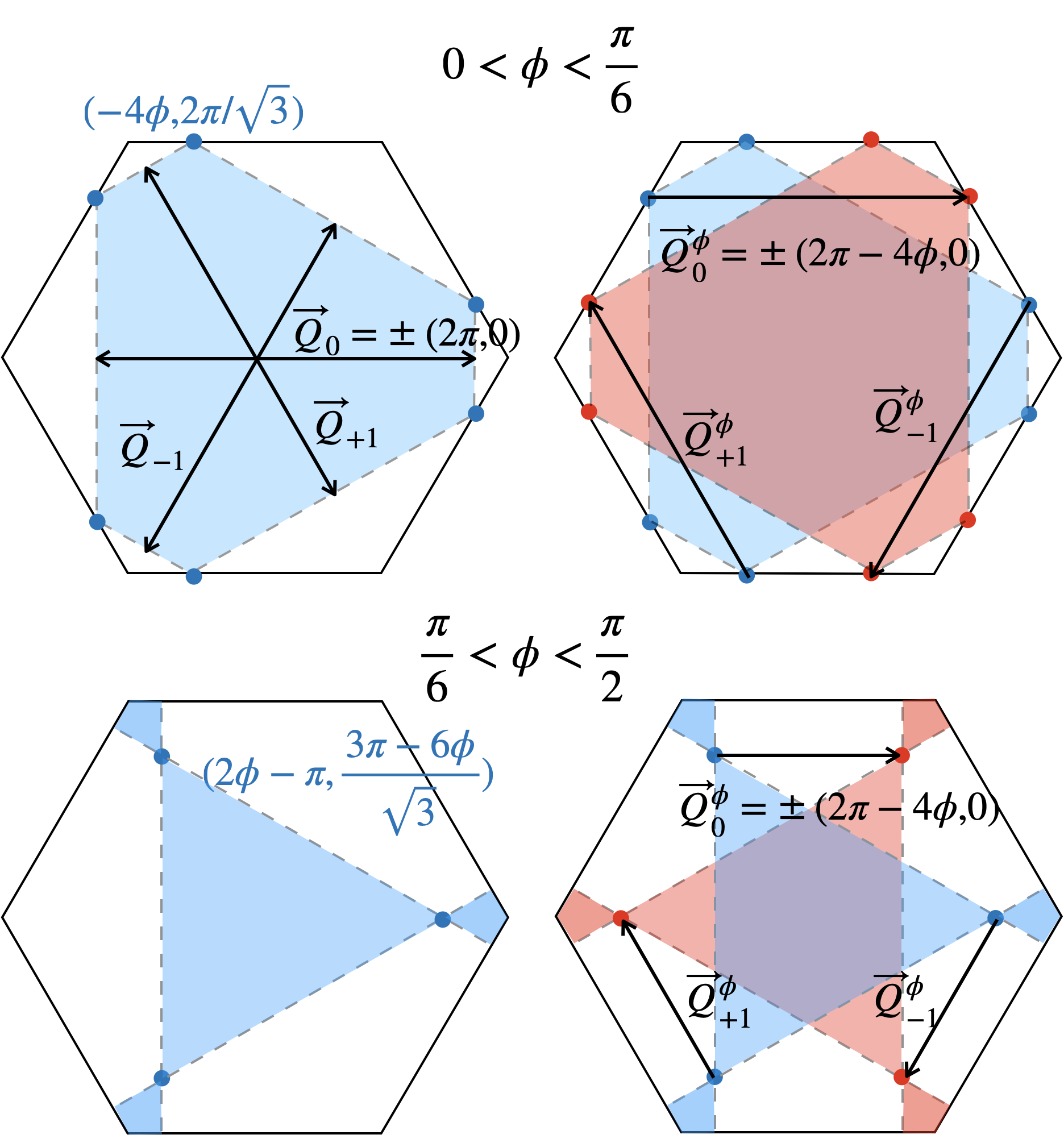
- “Moire” materials, consisting of atomically thin sheets stacked at small relative twist angles exhibit many remarkable properties, including topological, strongly correlated and superconducting phases of matter. Their properties can be tuned through readily accessible external parameters including gating, straining, packing and twist angles, making the systems robust quantum simulation platforms for the study of strongly correlated physics and topology in quantum materials and the creation of new device functionalities. At CCQ and in collaboration with theoretical and experimental groups world-wide we are studying the novel physics of these systems.
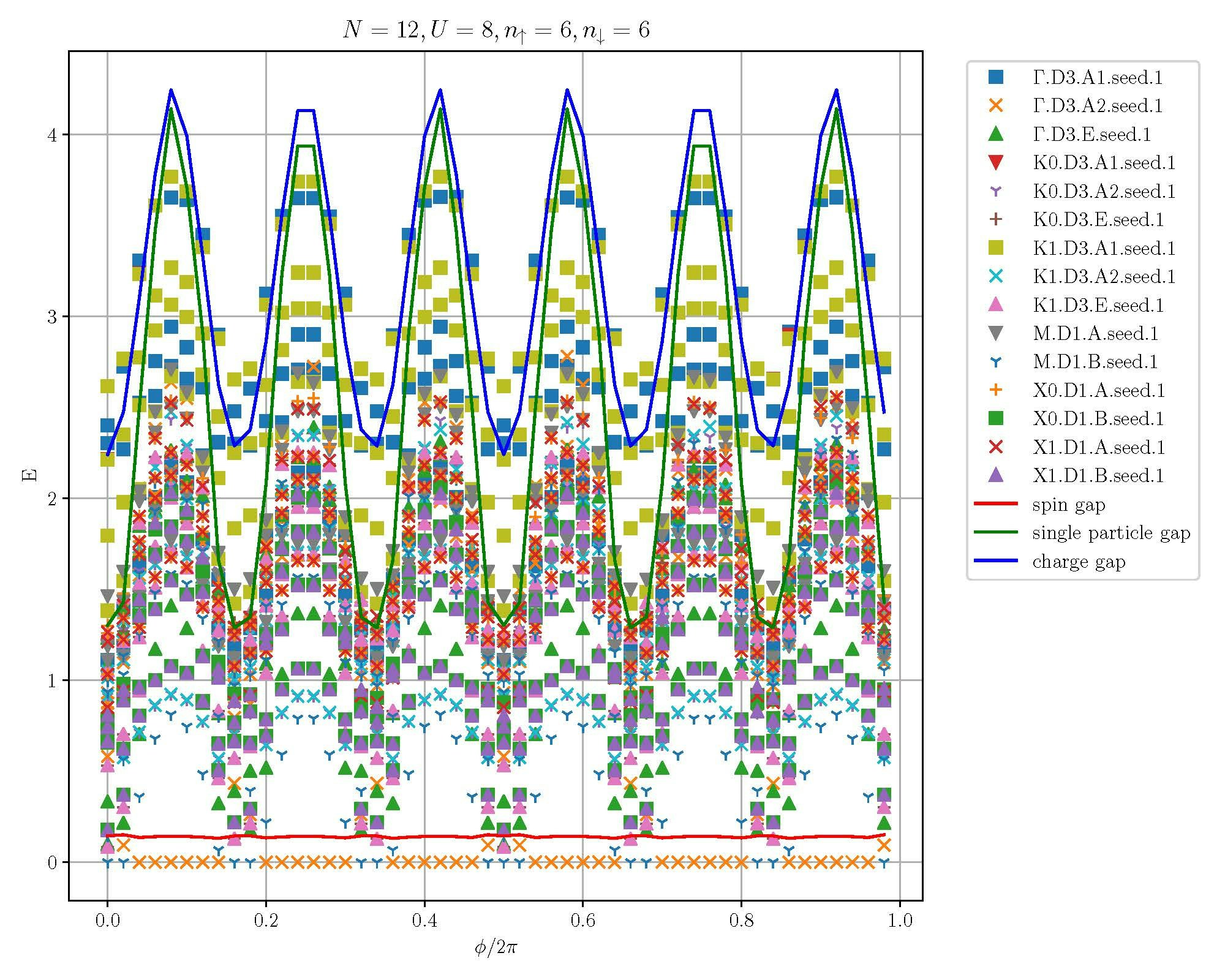
Current projects include quantum criticality and correlated phases in twisted WSe2 (a realization of the spin-orbit coupled triangular lattice Hubbard model) and analysis of interaction effects and band geometry in twisted bilayer graphene.
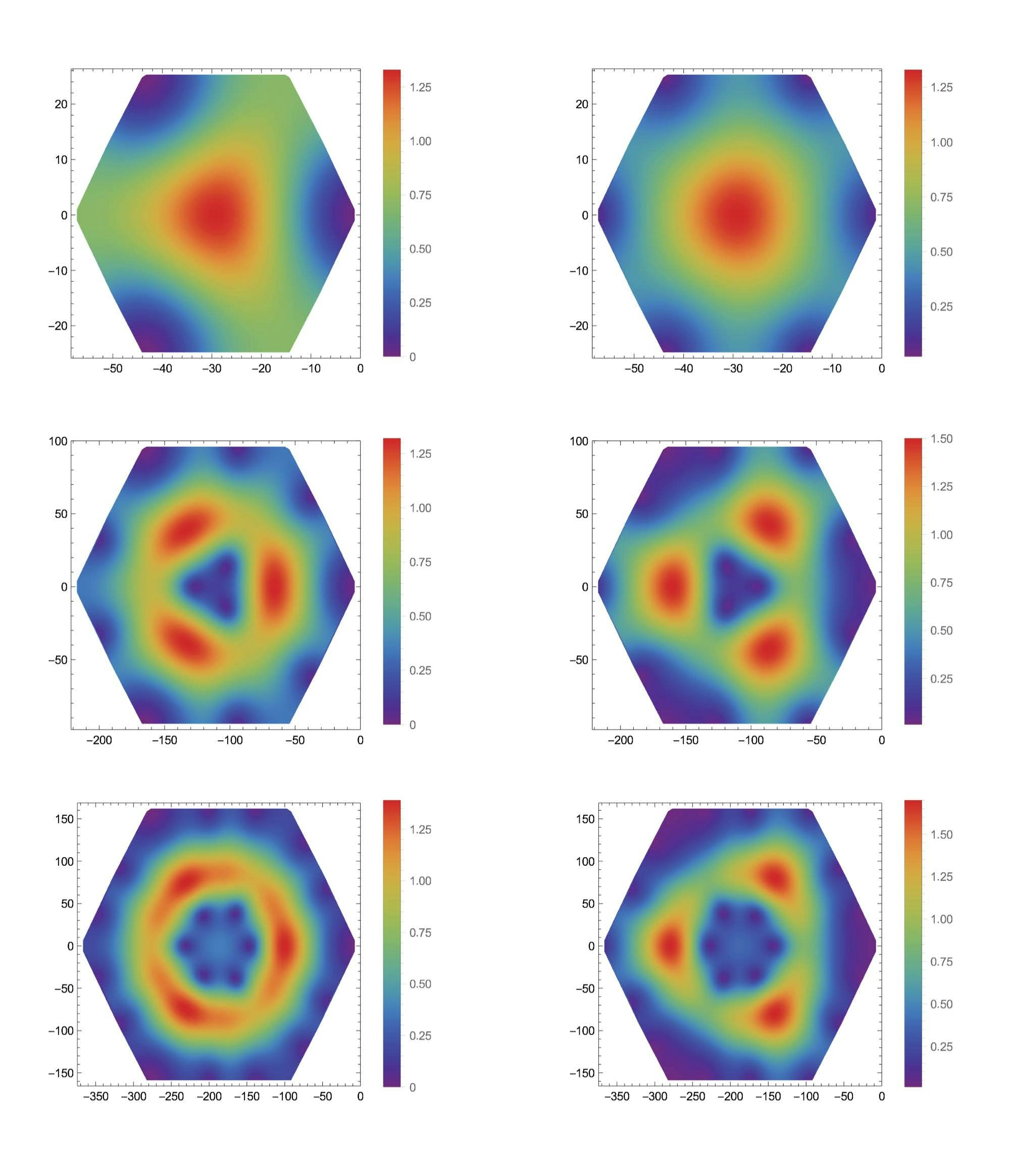
References
- Modular Arithmetic with Nodal Lines: Drumhead Surface States in ZrSiTe, Lukas Muechler, Andreas Topp, Raquel Queiroz, Maxim Krivenkov, Andrei Varykhalov, Jennifer Cano, Christian R. Ast, and Leslie M. Schoop, PhysRevX.10.011026
- Moiré superlattice on the surface of a topological insulator, Jennifer Cano, Shiang Fang, J. H. Pixley, and Justin H. Wilson, PhysRevB.103.155157
- Moiré heterostructures as a condensed-matter quantum simulator, Kennes, D.M., Claassen, M., Xian, L. et al., Nature Physics 17, 155 (2021)
- Chiral approximation to twisted bilayer graphene: Exact intravalley inversion symmetry, nodal structure, and implications for higher magic angles, Jie Wang, Yunqin Zheng, Andrew J. Millis, and Jennifer Cano, PhysRevResearch.3.023155
- Exact Landau Level Description of Geometry and Interaction in a Flatband, Jie Wang, Jennifer Cano, Andrew J. Millis, Zhao Liu, Bo Yang, arXiv:2105.07491
- Hartree-Fock Study of the Moiré Hubbard Model for Twisted Bilayer Transition Metal Dichalcogenides, Jiawei Zang, Jie Wang, Jennifer Cano, Andrew J. Millis, arXiv:2105.11883
Project Leader: Andrew Millis
Project Scientist: Jungho Daniel Choi, Valentin Crepel, Antoine Georges, Daniele Guerci, Angel Rubio, Yubo Paul Yang