Q&A: Finding Structure in Neural Activity

Neuroscientists first described head direction cells — neurons that represent the direction an animal’s head is facing — in the 1980s. The first models for how they work emerged about a decade later. But it’s only in the last few years that researchers have been able to gather enough neural-activity data to truly test those models. New technologies capable of recording neural activity from hundreds of cells simultaneously have made it possible to study neural circuits in more detail than ever before. With a combination of experimental and theoretical tools, researchers are now trying to decipher how groups of neurons work together to represent information, make decisions and perform other computations.
Of particular interest to Ila Fiete, a neuroscientist at the Massachusetts Institute of Technology, are neural circuit dynamics — how patterns of activity in populations of neurons evolve over time while solving computational problems. These dynamics are thought to underlie the brain’s immense computing power, making it fast and flexible. In June, Fiete and Gilles Laurent, a neuroscientist at the Max Planck Institute for Brain Research in Frankfurt, Germany, organized a conference, “Dynamics of the Brain: Temporal Aspects of Computation,” to explore how researchers are using new approaches to study circuit dynamics and their role in neural computation.
Fiete, an investigator with the Simons Collaboration on the Global Brain, talked with the SCGB about how this onslaught of data is creating new opportunities in the field and sparking a growing dialogue between experimentalists and theorists. An edited version of the conversation follows.
What inspired you to organize this conference?
Dynamics have long been an area of great interest to Gilles Laurent. He has been a pioneer in viewing neural computation through the lens of how the states of the circuit evolve over time. For me, as a theorist who builds mechanistic network models of neural circuits, it is of deep interest to compare dynamics in models and brains. Because of recent experimental and theoretical developments, the time was right to bring people together on this topic. The tools for measuring neural activity are now catching up enough with the theory that we can look for the dynamics predicted by models in actual brains.
For example, I work on the head direction circuit. This circuit receives information from a lot of sensory modalities, including visual and vestibular cues that must be distilled into an estimate of how fast the animal is turning, then converted into an updated estimate of which way the animal is facing in the world. The theory to explain how this circuit encodes head direction is mathematically elegant — and two to three decades old. Now we finally have the methods and data to address whether or not the data match up with the models.
The conference is called “Dynamics of the Brain: Temporal Aspects of Computation.” What do you mean by dynamics?
We are talking about how the neurons in a circuit interact to generate something entirely new relative to what single neurons could do on their own. Until recently, it’s been difficult to probe circuit-level dynamics at single-cell resolution. Now, with calcium imaging and probes that can record from hundreds of cells, we can record from a good fraction of the circuit and examine how circuit response changes over the course of a single computation. Circuit-level interactions are important because we think a lot of neural computation emerges at that level. For example, if a single neuron receives an input, it responds but quickly forgets, returning to baseline activity as soon as the input is removed. If neurons in a circuit can drive activity among themselves, they can collectively hold on to a memory of a transient input long after it is gone.
Can you give an example of a neural circuit that researchers are exploring from a dynamics perspective?
One example from the conference was Gilles’ work on the chromatophore system in squid, a system of pigment-containing cells that the animal controls to rapidly change its skin patterning. The animal looks at the environment and makes a decision about what pattern to project onto its skin to camouflage itself, attract a mate, scare a competitor, etc. It then directs those motor-controlled chromatophores to create the appropriate pattern. That’s an example of a sensory system that has to take in lots of time-varying sensory data, make a decision, and produce a response. The response is the projection of that decision onto a high-dimensional space — the activity patterns of thousands of chromatophore cells. The animal must keep revisiting that decision and adjusting its outputs as the sensory and social context changes. This system raises a number of interesting dynamics questions. How much freedom is there in the patterns an animal can express? Can it express arbitrary patterns? Do lateral interactions among cells restrict the set of possible patterns? What constraints are there on the system in space (types of patterns) and time (how quickly they change)?
By clicking to watch this video, you agree to our privacy policy.
What are some of the most important themes to emerge from the talks?
We heard a lot about low-dimensional manifolds and dynamics. A circuit of 1,000 neurons could theoretically produce 1,000-dimensional activity — one dimension for each neuron. But in reality, circuit activity is often confined to a much lower-dimensional space. Basically, low-dimensional representations mean that the brain has created a simple summary of what’s important in the world. (For more on manifolds, see “Searching for the Hidden Factors Underlying the Neural Code.”) Across different types of cognitive circuits, we’re seeing the existence of low-dimensional organizing structures that represent information relevant for behavior and perception. For example, researchers have long sought simpler organizing principles for how the olfactory system represents odors, but such structures have been difficult to find. In an exciting new chapter in that quest, Bob Datta of Harvard University presented beautiful work revealing that the mouse olfactory system represents information in a relatively low-dimensional map space, based on a few salient chemical properties of odorants — chain length and chemical family.
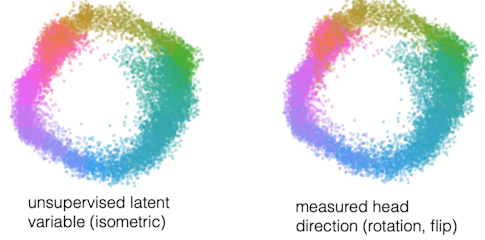
Rishidev Chaudhuri, a former member of my group now at the University of California, Davis, has shown that the head direction circuit, which contains a few thousand cells in rodents, generates a one-dimensional ring that exactly corresponds to an internal compass representing which way the animal is facing. Even when the animal is asleep, there are internally organized constraints on activity that keep the system one-dimensional. (For more on this circuit, see Chaudhuri, Fiete and collaborators’ new paper in Nature Neuroscience.)
Why does the brain constrain neural activity this way?
Low-dimensional representations are an abstraction: They take massive volumes of data and extract the essential variable for a given computation. They give robustness or stability, which is important both for memory and for reducing noise. Each neuron in the circuit fires with some level of noise, potentially pushing the system to some other part of high-dimensional space. If the system is forced to occupy low-dimensional states, it means the system automatically removes these other dimensions, reducing the effects of noise — in other words, it’s a device for error correction, or de-noising.
Coupling neurons together to form stable low-dimensional states also enables them to hold on to this set of states or patterns over time, which is the basis for memory. The importance of each of these functions — noise reduction versus memory — varies from system to system. For a low-level sensory system, the error-correction piece is probably most important. For an integrator system or evidence accumulator, both are important.
For head direction, for example, the brain decided to devote a circuit of 2,000 neurons to this one-dimensional variable. You can represent a lot of information with 2,000 neurons — if each neuron acts independently, the activity of the population as a whole occupies a 2,000-dimensional space — so shrinking the representation down to one dimension seems wasteful. But confining the representation to one dimension kills the noise. That is especially important for the head direction system, which integrates lots of signals and accumulates noise in each time step. Integration over time also requires memory — remembering which way the head was pointing before adding the most recent updates to get the current heading direction.
Why does the head direction circuit use so many cells to represent a one-dimensional variable? Just to get rid of noise?
I’m obsessed with this question. It’s one we couldn’t even ask until now. We used to think that maybe those 2,000 cells were encoding something in addition to head direction and that’s why there are so many cells. But now, by looking at the manifold, we know it’s one-dimensional, meaning that this population of neurons is representing just one variable. So why does the brain have specifically 2,000 neurons for this one variable? I am excited because this is a super concrete and quantitative question. Until now, theoretical neuroscience has been forced to deal with only qualitative questions and answers, but we are at the precipice of becoming a quantitative discipline.
What were some surprising findings from the meeting?
Datta’s olfactory maps were pretty amazing. The finding that there is a well-ordered map, at least for this specific family of odors, is amazing. It’s one of those things like, how did we not know this? An exciting body of work from Mala Murthy’s lab at Princeton University was the simultaneous and continuous monitoring of behavior and brain activity across areas in the fly during courtship singing behaviors, together with post-mortem full-brain connectivity analysis. (For more on work from the Murthy lab, see “How Fruit Flies Woo a Mate.”) This work, as well as the work on chromatophores in the Laurent lab and songbird auditory and vocal circuits in Sarah Woolley’s lab at Columbia University and Michale Fee’s lab at MIT, simultaneously inspires and brings into relief the challenges ahead of us in understanding how moment-to-moment behavior shapes, and is shaped by, the underlying neural activity, and how in turn that neural activity emerges from connectivity in the brain. (For more on work from the Fee lab, see “Finding Neural Patterns in the Din” and “Song Learning in Birds Shown to Depend on Recycling of Neural Signals.”)
How is the field evolving?
For a long time, ideas about the collective behavior of circuits were largely theoretical. But now, with experiments that generate real-time data across the circuit, we can build bridges between experiment and theory. Large data has also led to a growing appreciation of computational approaches among experimentalists. Experimentalists seek out more mathematical training, as they recognize the urgent need to develop ways to analyze this data. As experiments become more quantitative, experimentalists and theorists are forming a common language, which is leading to a lot more dialogue.
How can the field enhance communication between experimentalists and theorists even further?
I think machine learning has been a boon for that — experimentalists and theorists are starting to learn the same language through the use of machine learning tools. There are more and more summer schools on computational neuroscience in the U.S., Europe and Asia, which I also think is really helpful. And there is more training in computational approaches at the individual university level: At MIT, for instance, we run a methods-based journal club over the summer, where we read papers that use certain methods and then have hands-on coding sessions to try them out. It helps a lot to have experimentalists and theorists sit side by side.
What big questions should the field tackle next?
I’m interested in the interplay between the dynamics of circuits when they are driven by inputs compared to their internal dynamics, such as the dynamics that occur when an animal is sleeping and getting no external sensory information. For understanding computation in the brain, it’s important to understand how a circuit can be low-dimensional for one task and low-dimensional in some other way on another set of tasks. How do these dynamics fit together? How does the system do different tasks at different times in a way that is stable and doesn’t cause interference? How is the dimensionality in response to inputs driven by connectivity of circuits and internal constraints? We need a mathematical theory of how multiple low-dimensional dynamical systems coexist in a single circuit and interact with each other. How do they transfer information to each other?
Is this something you or others are working on?
People are starting to think about this. New technologies enable us to look at neurons in multiple brain areas simultaneously, so we can ask in a quantitative way how different areas affect each other. The International Brain Lab [a project co-funded by the Simons Foundation and the Wellcome Trust] and the BRAIN Cogs project at Princeton, led by Carlos Brody and David Tank, are two examples of groups tackling these kinds of questions.
What advice would you give students who are interested in this field?
I would tell them to learn as much math as they can — we are surely going to need new tools and ways of thinking mathematically to answer these questions. What I know is never enough! But the beauty of a scientific training is that we learn how to learn what we need to learn along the way.


