Quantum Monte Carlo

A digital illustration of four silver spheres contained within 3 concentric circles made up of white dotted lines. The outermost circles of the middle-left and middle-right spheres have partially merged to each other. The leftmost edge of the leftmost circle and the rightmost edge of the rightmost circle stretch towards something outside of the frame of the picture. There are white wavy dotted lines above and below the set of spheres and circles. Finally, each of the four spheres is set against its own yellow radial gradient, giving the impression that the spheres are — Motta et. al., Phys. Rev. X (2020)

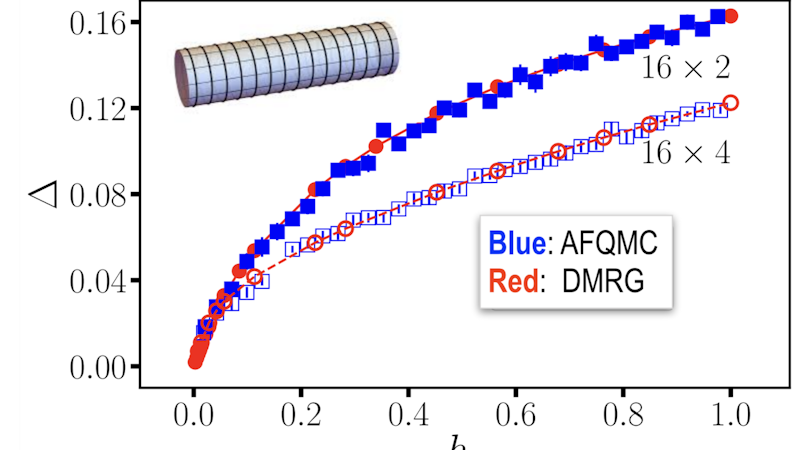
A line graph containing red and blue lines made up of either circles or squares. A panel in the graph contains text that reads — Motta et. al., Phys. Rev. X (2020)

Quantum Monte Carlo (QMC) is an umbrella term that refers to computational methods using stochastic sampling in some form to study quantum systems. A key characteristic of the quantum many-body problem is the high dimensionality of the Hilbert space involved. QMC methods thus have an integral role in CCQ activities and spans a wide range of algorithms: formulating the solution of the Schrodinger equation directly as random walks in a manifold of Slater determinants (auxiliary-field quantum Monte Carlo, or AFQMC); evaluating expectation values of a given many-body wave function ansatz to minimize the energy with respect to many parameters (variational Monte Carlo, often used in combination with machine learning); performing sums of Feynman diagrams in a perturbative expansion (diagrammatic Monte Carlo); using Monte Carlo as a solver to a smaller impurity problem embedded in a larger medium (in combination with dynamical mean-field theory); summing the trace over many-body states derived from tensor networks (referred to as minimally entangled typical thermal state or METTS); etc.

Our effort is anchored by both methodological innovations and software developments. They are in turn applied to problems ranging from understanding model systems for exotic quantum states to ab initio calculations in molecules and solids.

Project Leader: Shiwei Zhang, Miguel Morales

Project Scientists: Brandon Kyle Eskridge, Chunhan Feng, Ryan Levy, Yubo (Paul) Yang, Chia-Nan Yeh