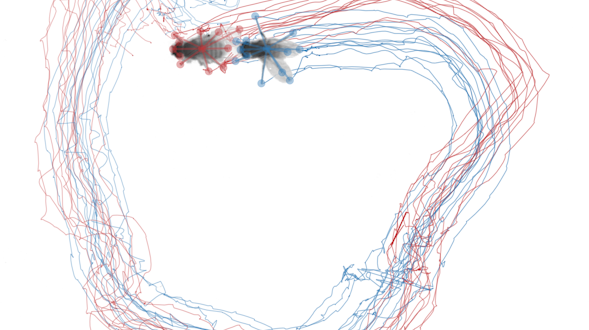
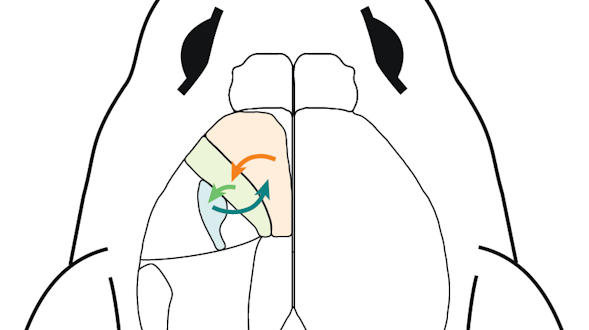
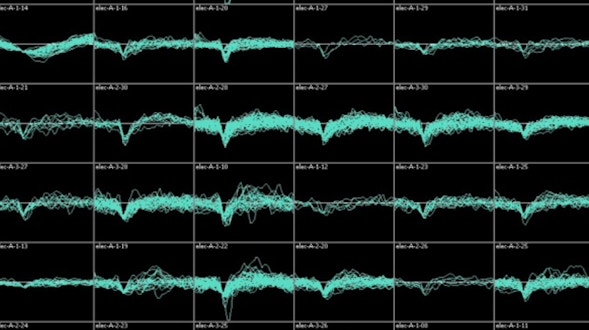
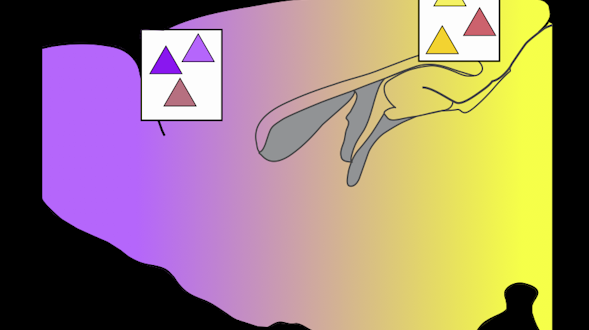
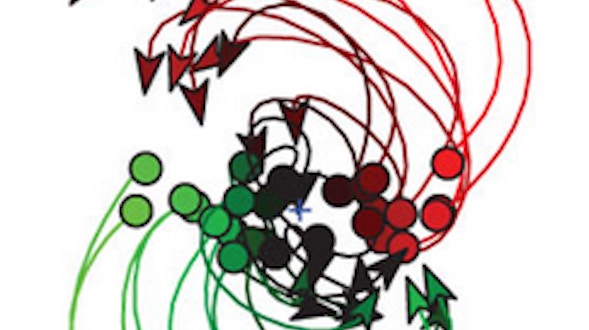
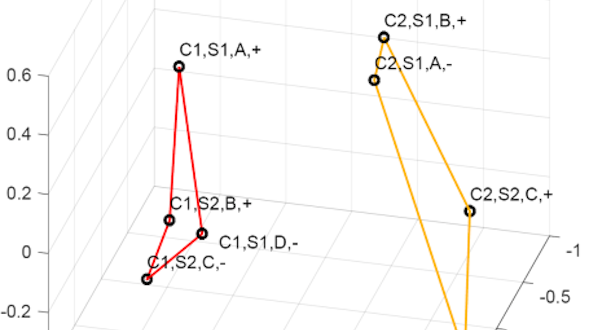
Communication is a fundamental aspect of life among animals, and yet we lack a comprehensive understanding of the underlying neural mechanisms. During communication, brains process sensory cues of different modalities, integrate those cues over time relative to changing internal states, and continually adjust ongoing actions. Here, we propose an ambitious, collaborative project to examine how the complete wiring diagram of a brain gives rise to brainwide patterns of activity that shape a social interaction, from sensation to action. In particular, we will leverage a novel connectomic resource and functional imaging methods uniquely available for Drosophila, combined with recent breakthroughs in deep learning and statistical methods for analyzing neural and behavioral data, to investigate how a female fly dynamically communicates with her social partner during courtship.
Projects
Movement is the primary way animals interact with the world. To produce the incredibly adaptable and complex behavior of mammals, many areas of the brain must work together to generate control signals and incorporate feedback. Yet because feedback is extensive throughout these circuits, it’s a challenge to understand the differential roles of heavily connected areas, and to tease apart what information is inherited from inputs, what is computed locally, and what is fed back from downstream areas. To tackle the question of information flow and inter-area communication, we will link three complementary approaches in the mouse: advanced behavior, state-space methods and projection tracing.
Every time we open our eyes, we take in far too much visual information for our brains to fully process. To cope with this issue, our brains have learned to pick out the most important details in a visual scene and quickly decide how to act on that information.
That process requires multiple components — some parts of the brain encode sensory information, some parts retain this information while making a decision, and some parts decode sensory and cognitive information in order to act upon it. We want to determine how parts of the brain encode information, relay it to one another, and decode it, which is fundamental to proper brain function. We will record the electrical activity in the brains as animals perform a visual decision-making task. Because we can simultaneously record from many neurons in different parts of the brain at once, we can analyze how these different regions communicate with one another. For example, brain activity patterns vary even when perceiving the same stimulus or making the same movement. How does this variation influence how one part of the brain communicates to another? How does communication change depending on the internal state of the animal or the nature of the task? Do these changes enhance learning or other cognitive functions? We will then build computer models of neural networks in the cortex and compare those models to our data. Our models can simulate how brain areas process information before passing it along and how different processing strategies would affect transmission across the brain. We can then compare our predictions to the data observed in our recordings. We anticipate these fundamental discoveries will be broadly applicable to any species, including humans.
The ability to make decisions lies at the core of cognition, but much remains unknown about its underlying neural mechanisms. Progress has been hindered in part by the fact that decisions vary widely in terms of the underlying computations (e.g., stimulus processing, memory) and their timescales (split seconds, minutes). Until recently, another hurdle was our limited ability to record neural dynamics at large scales. Thus, most of what we know about decision-making has come from studies focusing on the role of single regions during single tasks. Yet it has become increasingly clear that decision-making is supported by distributed cortical dynamics. However, we still do not understand how the features of distributed dynamics vary as a function of the types and timescales of cognitive computations underlying particular decisions. We aim to fill this gap by recording and perturbing neural dynamics across the cortex with mesoscale or cellular resolution, over a parameterized task space of decision-making computations and the timescales thereof.
The human brain is a daunting object: It contains nearly 100 billion neurons, each one linked to roughly 10,000 other neurons, making 100 trillion total connections in the brain. To make matters more complicated, each neuron can fire up to hundreds of times per second.
Understanding this blizzard of activity is one of science’s final frontiers. The brain’s basic functions — such as planning, decision-making, and behavior — require multiple brain areas and many thousands or millions of neurons, generating complex patterns of neural activity. Determining what aspects of this ever-changing activity are relevant for the task at hand, and how it ultimately leads to thoughts and behavior, can appear as an insurmountable challenge. One may think that studying very simple behaviors will help us solve this challenge. However, the opposite may true — the solution could lie in making the tasks we study more complex. By studying how the brain solves the same problem in many different settings, our group aims to better distinguish the relevant, invariant components of brain activity — those that are common to all settings — from components that are variable and thus not critical to the task at hand. We seek to develop a mathematical framework that can explain how invariant components emerge from the seeming chaos of neural activity and how their dynamics implement the computations necessary to drive behavior. We refer to this framework as ‘computation-through-dynamics.’ We will ensure our mathematical descriptions remain faithful to the reality of the brain by tightly integrating experimental and theoretical approaches within our group. With this interdisciplinary approach, we hope to make the task of understanding the human brain’s 100 billion neurons a little more tractable.
Imagine a tennis player hitting a forehand, but in slow-motion: There is anticipatory footwork, alignment of the body, preparation of the racquet, the wind-up and swing of the arm, final adjustments as the ball approaches, contact and a follow-through. Sports coaches and players intuitively learn and divide this complex behavior into discrete steps.
Players will drill the footwork, the swing and the follow-through separately. This general principle — that an action can be divided into a series of steps — holds true for any movement we do. However, the smallest meaningful units of behavior remain a mystery. Taking inspiration from linguists, who view spoken words as syllables that can be infinitely recombined, we seek to discover the ‘syllables’ of behavior — and the patterns of brain activity that generate them. We will take advantage of new technology to automatically track the movements and body position of a mouse as it forages around its cage and performs tasks. At the same time, we will monitor the activity of a brain region called the striatum, which is involved in rewards, movements and cognition. Using a new class of mathematical models that do not make many assumptions about how behavior is organized, we will deconstruct the mouse’s normal behavior into motifs, or syllables, and correlate those with brain activity. The striatum is especially interesting to monitor because it receives inputs from the brain’s dopamine system. Recent work suggests that the dopamine system initiates the switch from one behavior to another, providing the basis for how syllables are recombined to create an infinite repertoire of behavior. Our results not only will illuminate how a laboratory mouse behaves but might one day even explain how a professional tennis player hits a forehand.
Imagine you are rowing a boat in a river. If the boat stops moving relative to the shore, you might conclude that the river’s current has picked up and decide to row harder. That decision results from a combination of sensory information and internal predictions.
Your brain compared your actual position to your expected position given how fast you were rowing and concluded that the slowing of the boat violated your sensory expectations. Every time we navigate through the world, we not only carry out the current movement but also predict how our sensory environment should change when we move. How the brain does this is largely unknown. We hypothesize that you can use your past position and current velocity to create what we call your ‘episodic state’ — the minimum knowledge of the past and present needed to predict the sensory experience of the immediate future. We will test this hypothesis by recording activity in many neurons, in both mice and flies, as the animals navigate a virtual reality environment. With virtual reality, we can create situations in which the laws of physics hold or are violated. For example, physics dictates that if you move the same amount forward as backward at the same speed, you should end up in the same place. We can break this rule and see how the animal — and its brain — responds. This setup allows us to determine how the brain computes its position and velocity, how it creates a representation of its episodic state and how it uses this information to predict future sensory feedback. This work will provide general insights into how any animal makes predictions, including humans.
FULL PROJECT
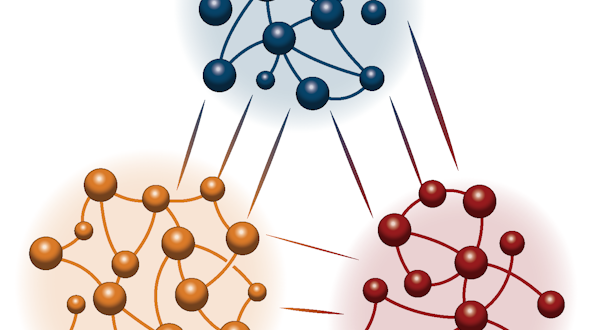
Behaviors are known to arise from numerous neurons communicating with each other within and across brain areas. Less is known about the precise nature of long-range neural interactions that give rise to global activity patterns in the brain during behavior. Recent advances in experimental and computational techniques present the opportunity to examine such interactions at an unprecedented level of detail. In this project, we will investigate cell-type-specific interactions among three brain areas involved in motor control. This will be done in a close collaboration between computational and experimental groups at the University of California, San Diego.
The brain has a remarkable ability to choose appropriate actions in the face of an ever-changing environment. Even when sensory input is completely new — such as being in a new environment — animals are able to navigate successfully, respond to threats and capture prey.
This ability depends on integrating sensory input with past experience to make decisions and implement behavior. Neuroscientists have long sought to understand how the brain makes complex decisions in uncertain environments. Recent technical advances have produced huge amounts of brain activity data recorded as animal perform these types of tasks, yet neuroscientists have developed relatively few new theories to explain these data. We have established a collaborative group to develop mathematical descriptions of brain activity called ‘dynamical neural models.’ Dynamical neural models help explain how the activity of hundreds or even millions of neurons represent internal variables — a sound, the position of a limb during a movement, the desire to move in the first place, or something else. We will study how groups of neurons pass messages to each other to create these representations, as well as how the brain learns to form them and use them for decisions and actions. Our work will provide much-needed theories of brain function to help interpret the large amounts of data generated by neuroscientists.
Prediction of the future and mental simulation of experiences are key to many forms of cognition and sensory processing. Humans (and likely also other animals) use mental simulation to evaluate candidate behavioral choices. Predictions of upcoming sensory events and how they relate to planned motor actions seem vital to motor choreography and the ability to properly interpret sensory data during active movement. Motivating our work is the idea that the cortex likely uses a core set of computational approaches and mechanisms that are conserved across multiple forms of future prediction. We conjecture that the cortex uses, in many contexts, a general strategy for jointly encoding and processing sensory and motor data for the sake of predicting future outcomes, deciphering sensory evidence in light of self-actions, and intelligently navigating the world.
The human brain is composed of billions of neurons. Currently, neuroscientists understand just a fraction of the electrical and chemical code that neurons use to communicate with one another. One obstacle has been the lack of technologies to simultaneously track the activity of each individual neuron at ‘the speed of thought.’
New techniques, however, are on the verge of accomplishing this in smaller systems. Our group will combine the power of sophisticated computer algorithms with cutting-edge microscopes to monitor the activity of many neurons at once in real time. Our previous work used powerful microscopes to observe all the neurons in the brain of a zebrafish in its larval stage. However, these observations were slower than the speed of electrical activity in the fish’s brain. Collaborating with other labs, we will develop computational methods to determine the activity of single neurons even when the microscope on its own isn’t powerful enough to view objects as small as single cells. This advance will enhance imaging speed up to tenfold or more, enabling us to conduct previously impossible experiments. Working in zebrafish, for example, we will identify how small areas of the brain involved in initiating movements influence how the entire brain processes feedback from those movements. Our work will provide a suite of new tools for other neuroscientists to use, as well as general insight into how the brain processes information and carries out behavior.
The adaptive value of cognition manifests in decisions not only about how to act but also about when to act. Though much neuroscientific investigation of decision-making has focused on sensory-guided perceptual decisions, somewhat distinct neural processes appear to underlie internally generated (self-driven) decisions of when to act.
A central goal of neuroscience is to decode the brain activity responsible for decisions and actions. Imagine an animal foraging for food. First, the animal needs to evaluate sensory signals in its environment to judge which foods are currently available.
Then, the animal must decide which of the available food choices will be the most rewarding and make a plan for action. The neural mechanisms supporting that seemingly simple process are frighteningly complex. Until very recently, the field has lacked the tools to read out neural activity at the scale necessary to understand even the simplest choices. A recent explosion in new techniques and accompanying mathematical advances has opened a window into how the brain makes choices. But a serious challenge remains. Harnessing these new tools effectively is beyond the reach of any single laboratory. While individual labs have made significant advances, the piecemeal approach has so far made it difficult for scientists to compare and reproduce each other’s data. The International Brain Lab, a joint effort funded by the Simons Foundation and the Wellcome Trust, will combine the efforts of 20 laboratories worldwide to focus on a single goal: to determine how the brain functions during a simple decision in a mouse. The mouse will be trained to make decisions about visual stimuli while we measure neural activity brain-wide. We will make precise electrical recordings of hundreds of neurons from many brain areas and use sophisticated microscopes to directly observe the brain in action. Leading computational neuroscientists will develop mathematical and computer models of this brain activity. We hope not only to discover how brains support decision-making in any animal, humans included, but also to offer a new large-scale, collaborative model for brain science.
Humans and other animals can rapidly solve new problems — such as imitating a dance from a single observation — by adaptively combining components from prior knowledge to generate new thoughts or action plans. This ability, compositionality, is central to intelligence. Yet its neural mechanisms are unknown. Cognitive models suggest an important role for symbolic knowledge in compositionality: abstract structures and algorithms to support extrapolative reasoning. Despite the success of these models, we do not know whether or how symbolic computations are implemented in the brain. Bridging this gap between symbols and neurons would be a critical advance toward explaining mechanisms of compositionality. To this end, we have developed a new animal behavioral paradigm for compositional reasoning, and we will uncover its underlying neural mechanisms by combining neurophysiology with cognitive and neural network modeling.
Animals often move in response to the senses. A dog follows a scent trail or a field mouse seeks cover after a hawk’s shadow passes overhead. Neuroscientists studying the sensory system have made great strides decoding how the brain translates sights and smells into neural activity.
They give animals a specific stimulus — a pattern of stripes, say, or a specific chemical odor — and simultaneously measure the brain’s ‘code’ for that stimulus: i.e., how neural activity depends upon the stimulus. However, this approach has largely failed for the brain’s output side, the motor system. Despite decades of work, neuroscientists still struggle to describe how neural activity in the brain relates to the movements being generated. The number of neurons in the brain’s motor areas vastly exceeds the number of muscles, meaning that many different patterns of neural activity could be responsible for the same movement. This makes it potentially impossible to find a unique, simple code describing neural activity in terms of movement. Our goal is to turn this conundrum into an opportunity. Of all the patterns of neural activity that could produce a given movement, the brain must pick one, and this ‘choice’ may be illuminating regarding the basic principles at play. Using a combination of experiments and computer modeling, we aim to describe the choices made by the brain’s movement-generating system, and to decipher the principles behind those choices. We will train monkeys to use their arms to control a pedal-like device and navigate a virtual world for juice reward. At the same time, we will record the activity of neurons in the motor cortex and muscles in the arms. Pedaling movements have predictable properties — they are smooth and occur in cycles of varying speeds. Yet pedaling is driven by complex patterns of muscle activity that the brain must precisely create and control to ensure smooth movement. By comparing muscle activity to neural activity across many such movements, we can employ mathematics and computer optimizations to ask why the brain ‘chooses’ the observed patterns of neural activity. Neural network models can then be used to ask whether and why those choices are ‘good’ choices — i.e., do they allow the motor system to function better under challenging circumstances? Results will be compared between monkeys and mice. Indeed, we anticipate our approach will offer general insights into motor systems in any animal, including humans.
Our brains are able to store information about the world for several seconds after it was acquired, for example the shape and identity of an animal that disappeared behind a tree. Such ‘short-term memory’ is crucial for reasoning and decision-making, providing the link between past events and future behavior.
Despite its fundamental importance, how the brain represents and uses short-term memory is not fully understood. One of the challenges is that neural activity representing short-term memory is dispersed across different parts of the brain. Recent technological advances now allow us to measure activity from different regions simultaneously. We propose to study two different behaviors in mice that involve short-term memory. In the first task, a mouse will hear a sound and, after a delay, make a movement to report the sound it heard. The mouse has to maintain information related to the sound during the delay before indicating its decision. In the second task, we will present the mouse with a sound and then deliver another cue that will tell the mouse which actions to choose, contingent on the sound. Here the mouse has to retrieve past sensory information to make a current decision. We will use Neuropixels recording probes and a mesoscale microscope to record activity from hundreds of neurons in the brain. We will sample activity across approximately 50 brain areas, selected based on connectivity data. This data will amount to a map of neural activity underlying short-term memory, decision-making and movement initiation. The activity map will guide the development of computer models of the brain, allowing us to understand general rules of memory-guided decisions.
Some of our most complex behavior, such as speaking, swimming or playing the piano, can be understood by breaking the behavior down into a sequential succession of learning steps. This type of sequential learning is common across the animal kingdom — just as humans learn to speak, for example, songbirds learn to sing.
Decades of research have shown that many of the same neural processes can explain both behaviors. Birdsong, like human speech and other behaviors, is not innate but learned by imitating the behavior of parents and other adults. Scientists have identified neural circuits in zebra finches that drive song learning and have shown that the process requires the precise coordination of multiple regions spread across the brain. However, many questions remain about how these neural circuits develop throughout the bird’s lifetime. Previously, our lab demonstrated that a brain region called the HVC is involved in the timing of birdsong. Neurons in this brain region are individually active only at specific points in the song, but together form continuous sequences of activity that drive song production. We plan to observe the activity of neurons in the HVC and in auditory regions while juvenile birds are taught to sing by older adults, attempt the songs themselves and sleep. We’ll use this data to test the theory that sleep provides an essential stage of song learning — we hypothesize that the auditory regions of the brain replay the song while the birds sleep, activating the HVC to facilitate learning. Birdsong learning shares another remarkable feature with human speech learning. Juvenile finches babble just as human infants do — in birds, this is termed ‘subsong.’ We plan to investigate the brain areas, especially one called the LMAN, that drive subsong and provide the necessary variability for young birds to mix and match different sounds while learning to sing. We will collaborate with theoretical neuroscientists to develop and test models of how the brain forms sequences in HVC and generates the neural variability in LMAN. These advances will shed light not only on how birds learn to sing, but also possibly on how infants learn to speak, or how humans learn to perform any complex behavior based on sensory feedback, from sports to music.
When deciding whether to eat an apple, you might focus on its color, firmness and smell. If you’re about to throw it to a friend, you might note instead, perhaps unconsciously, its size and shape. This simple example illustrates a fundamental principle: we can use the same visual input to guide a variety of decisions and actions.
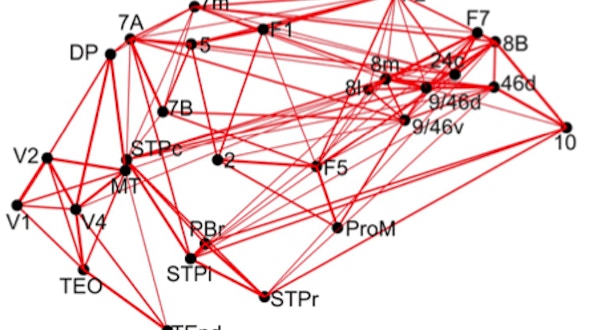
How the brain achieves this flexibility is unknown. We will try to answer this question by studying the part of the cortical visual system responsible for pattern recognition — the ‘ventral pathway’ — which serially elaborates the visual information needed to identify objects, and formats that information so that other parts of the brain can use it to guide decisions and actions. Each member of our team has separately helped to discover how different parts of the ventral pathway contribute to vision. Now we will team up to ask in broader terms how it works from end to end, and how it contributes to the performance of complex visual tasks. Working in monkeys — whose visual systems are very like our own — we will record the activity of neurons from many areas in the ventral pathway. In one family of experiments, we will use a consistent and comprehensive approach to study how the visual areas of the ventral pathway create visual representations that allow us to recognize and categorize the contents of our visual world. In a second family of experiments, we will ask how the information in these representations is used to support flexible behavior. For example, at one moment monkeys might be instructed to choose between different objects, say an apple and a banana. But in the next moment, the monkey might choose between different kinds of objects, say fruits (apple or banana) and vegetables. Thus the same visual stimuli can guide two different decisions depending on the situation, and our recordings will reveal the neural computations that underlie this capacity. While our ambitious experimental, model-building and theoretical endeavor is beyond the capacity of any one of us, we will be able to achieve it through the combined, collaborative effort of our team.
The brain of any animal has to operate on multiple timescales at once. In the long term, it has to evaluate the trade-offs between feeding, mating or conserving energy. In the medium term, the animal uses those calculations to create a plan — a hungry worm, for example, might choose to feed where it is rather than to go off in search of better food or mates.
In the near term, animals have to make immediate decisions about where to go, such as turning left or right or continuing on the current path. Studying how animals plan over these different timescales has been challenging, in large part because it requires many brain areas operating at once, and neuroscientists have lacked the tools to observe neural activity over broad swaths of the brain. To overcome this technical limitation, we will study the mating behavior of a simple animal, the tiny roundworm C. elegans. Roundworms find a mate by launching a systematic search of the environment, integrating scent and tactile information. Once the worm has found a potential mate, it begins a rudimentary sequence of actions that include turning, forward and backward movement, making contact, and finally copulation. The animal’s behavior is modified by long-term factors, such as natural cycles of activity and rest, whether its hungry or full, and the quality of food in the environment. We have developed a custom microscope to track the activity of almost every neuron in the roundworm’s head — here, we will perform the first whole-brain recordings in any animal during social interactions. Using this data, we will map the neural activity underlying long-term, internal states, such as hunger, and examine how that influences neural activity linked to medium-term behaviors, such as mating. We will combine neural activity and behavioral data with knowledge of the worm’s neural wiring to construct computer and mathematical models, from which we will learn how behavior is generated by neuronal activity, and how neuronal activity arises from neuronal network architectures. Because the wiring differs between the two sexes, we can also observe how sex-specific versus non-sex-specific behaviors arise in two variants of a nervous system. Our work in the lowly roundworm will shed light on how the nervous system processes information over multiple timescales with relevance for larger animals, including humans.
Context matters when making a decision. For example, we answer a ringing phone if we are in our own office but not in a colleague’s. This collaborative project studies how the brain learns about different contexts — ‘my office’ and ‘not my office’, for example — and how it uses context representations to guide decisions.
We will address these questions by training macaque monkeys to integrate sensory and contextual factors in well-controlled behavioral tasks. The monkeys will learn to follow specific rules based on the experimental context. We will record from different brain areas, including the prefrontal cortex, posterior parietal cortex, amygdala and hippocampus, as the animals perform the task. We hypothesize that the prefrontal cortex and amygdala will contain neural representations of the context in each task, while the hippocampus will play an important role in learning these contexts. We will test our hypothesis by applying different mathematical techniques, including dimensionality reduction, state space analyses, and neural network modeling, on our behavioral and neural datasets. These techniques enable us to extract context-related neural response patterns from the activity of hundreds of neurons within and across the recorded regions. Our results will offer insights into how context-based decisions are made in the primate brain.
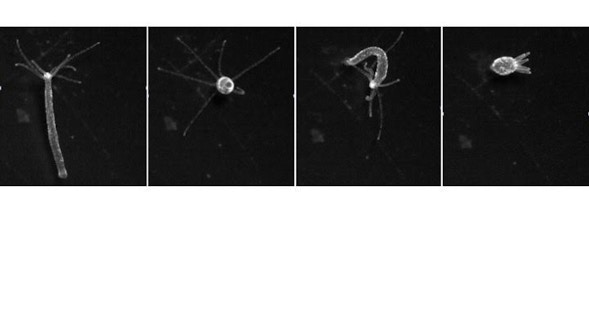
Our group is helping Rafael Yuste’s lab to pioneer the use of Hydra vulgaris, a small, freshwater polyp that attaches itself to underwater surfaces in lakes, rivers and ponds and uses its tentacles to capture prey, as a model organism for studying neural function. Hydra has a simple nervous system, a network of about 600 to 2,000 neurons, depending on the animal’s size.
(The human brain, in contrast, houses nearly 100 billion neurons). Despite its simple anatomy and tiny nervous system, Hydra boasts a dozen different behaviors: It can expand and contract, move its tentacles, and even somersault across surfaces. Until recently, scientists knew little about Hydra’s nervous system and had few technical tools with which to study it. We will develop techniques to track the activity of every neuron and muscle in Hydra, even when it is active (a challenge in Hydra, which can dramatically deform its soft body). We can disrupt or manipulate the activity of neurons and observe how that affects Hydra’s behavior. A detailed map, or connectome, of Hydra’s nervous system is in development, and we will take advantage of these advances to build near-complete computer models of its nervous system’s structure and function. How do distributed networks of neurons control behavior in a concerted manner? How do neurons sync up to control these behaviors? What types of connections are necessary for this synchronization? What does the ongoing activity in the nervous system mean even when the animal isn’t moving? Complete access to Hydra’s neurons will allow us to make headway on these questions. In addition, we will study another simple organism — the fruit fly — to elucidate how the entire brain coordinates behavior in the face of an ever-changing environment. Both Hydra and the fruit fly share a surprising number of basic neural building blocks with all animals, so we expect our insights will apply to any nervous system, humans included.
Loosely speaking, we all have two brains. Our ‘outer brain’ interacts with the surroundings via the senses or translates intentions into movements. Our ‘inner brain’ receives sensory information from the outer brain, integrates it with memories, internal states — such as hunger or arousal — and goals, then sends a plan of action back out to our muscles.
Each brain appears to process information distinctly, a phenomenon observed from flies to humans. Even devices using artificial intelligence, such as self-driving cars, have different ways of processing ‘outer’ and ‘inner’ data. That they are different makes intuitive sense. The outer brain has to deal with enormous amounts of data. Our eyes, for example, take in 1 gigabyte per second of raw image information, but we ultimately only use a fraction of that data. The inner brain, on the other hand, processes information at a far lower rate. Humans can speak, play piano or remember things at about 20 bits per second, meaning we can choose among a million possible thoughts per second. This is a lot, but pales in comparison to the information-processing task faced by the outer brain. While the outer brain excels at filtering relevant information, the inner brain excels at integrating information from the senses, our past experience and our internal state to decide and initiate an action. Traditionally, neuroscientists have studied one system or the other — inner or outer. We have assembled a team of five neuroscientists, each an expert in one region of the inner or outer brain, to bridge the gap. By performing related experiments in parallel and leveraging our combined expertise, we can examine how the inner and outer brains communicate with each other. We will explore whether the systems really use different processing strategies or if there are alternative explanations that do not require this dichotomy. Our work will investigate these questions in mice and humans and build computer models to test different theories. With a collaborative approach, we will determine the principles underlying the different brain systems, providing insight into human behavior and potentially enhancing artificial intelligence.
In the last few years, powerful experimental techniques that can monitor the activity of many neurons at once have generated a new field of neuroscience — ‘neural dynamics’ — which uses sophisticated mathematical models to describe how brain activity evolves on a moment-to-moment basis.
Research on how neural dynamics supports various computations has generally been conducted in a stable environment. We will study how the brain adapts, or ‘tunes,’ its dynamics to a changing environment. This distinction is crucial: If the brain cannot learn to alter its computations based on new or unexpected information, the animal is unlikely to survive. We will study how the neural dynamics controlling simple eye-movement behaviors in zebra fish and mice can be adaptively tuned to improve visual perception. Clear vision depends on the ability to hold the eyes stably on a given location when studying a feature of a stationary object or to move the eyes to accurately track moving objects. The ability to accurately hold the eyes at a given position is performed by a brain circuit called the ‘oculomotor integrator.’ We will study how the dynamics of this circuit are tuned by creating a virtual environment that simulates what an animal would see if, due to an improperly tuned oculomotor integrator, it could not accurately control the position of its eyes. We then will monitor and manipulate neurons throughout the eye-movement control regions to see how these networks adjust, or re-tune, their neural dynamics to adapt to the new environment. Finally, we will combine our data with detailed descriptions of the brain’s wiring and apply new mathematical techniques to analyze how the observed neural signals are processed and transformed by these brain circuits. By analyzing and comparing these two organisms, we can make general theories about how the brain adapts its activity to modify actions.
We take it for granted that we can distinguish similar events yet still group them together as being similar. Two concerts, for example, offer similar sensory experiences: They take place in large rooms with many people, typically with dimmed lights and loud music.
But there are also many differences — the design of the space, the identities of the crowd, and the quality of the music. Our brains face the challenging task of learning to group experiences by similarities — they were both ‘concerts’ — yet still distinguish them as two different events. One way that neural circuits might accomplish is this is via remapping, where the same neuron that encodes a memory, might, at a different time, encode location, time or sound. To gain insight into how the same neurons could encode multiple things, we will record brain activity in rodents and monkeys as they navigate different landscapes, such as an open field where they forage for food or a maze with multiple decision points. We will use novel recording technology capable of recording from the same neurons over time to determine how individual neurons shift their activity based on the environment and the task — in essence, the phenomenon of remapping. For example, the activity of the same neuron might reflect the rat’s heading direction when moving slowly, but its speed when moving quickly. In this case, the neuron has been remapped from direction to speed. We believe a similar process underlies how one neuron can be remapped from one memory to another. With this data, we can reconstruct the behavior of large neural circuits in brain areas involved in memory and navigation. Our group will collaborate with several other experimental and computational labs to develop the techniques and mathematical tools to gain insight into this fundamental brain process.
FULL PROJECT
Speech is a highly sophisticated, uniquely human behavior. It represents one of our fastest and most coordinated motor behaviors and connects intimately to higher-order cognitive capabilities of translating one’s mental state into sequences meant to influence another’s. Our groups have recently made headway in understanding the computations through neural ensemble dynamics underlying speech by piggybacking this scientific endeavor on top of an ongoing clinical trial studying brain-computer interfaces (BCIs) as a means to restore lost communication in people with paralysis. Here we propose extending this strategy to study how population activity (>100 neurons) in the ventral precentral gyrus (vPCG, i.e., speech motor cortex) and the pars opercularis portion of the inferior frontal gyrus (IFG, which encompasses Broca’s area) prepares and produces speech. We further propose complementing this high-resolution, narrow-windows ensemble single-unit-resolution study in two chronically implanted BCI participants with short-term medium-resolution, wide-coverage local field potential recordings across the wider speech and language network of multiple participants who are undergoing stereoelectroencephalography (sEEG) recordings, and with high-resolution, scattered-coverage recordings via sEEG wire tips and potentially with Neuropixels recordings during deep brain stimulation placement procedures.
Our interaction with the world is influenced by our internal state. A state of hunger makes us sensitive to images and smells of food that we might ignore right after a meal. More generally, the same sensory stimulus can lead to different behaviors depending on internal state.
It is currently unclear how internal state is represented and maintained within neural circuitry and how it acts to modify perception and behavior. We will study internal brain states in the fruit fly Drosophila melanogaster. Fruit flies are driven to eat by hunger related to various metabolic factors. We will examine whether and how these changes activate self-sustaining patterns of brain activity that represent internal state and heighten sensitivity to taste and smell and trigger food seeking. Using a new high-speed imaging technique called SCAPE to track activity in the entire fly brain, we will identify activity patterns that generate appetite and trigger food seeking behavior. We will also study a second important internal state in the fly, sexual arousal. Male flies become aroused when they sense certain chemical signals from a female, and this leads to courtship behavior that includes a song generated by wing vibration. The male keeps singing until the female decides to mate or decamp. This state of arousal involves neurons in the fly’s brain that respond to the female’s chemical signal and generate self-sustaining patterns of brain activity that persist well beyond the original sensory input. We will use imaging tools to record brain activity and analyze how a state of arousal triggers courtship behavior. Taken together, these lines of inquiry will offer insight into the poorly understood interplay of sensory input, internal state and action.
Working memory, the ability to temporarily hold and manipulate pieces of information in our minds, is crucial for thinking and flexible behavior. Scientists often study working memory in the lab by training subjects to make a response based on information from a few seconds in the past.
These ‘delayed response tasks’ suggest that working memory, at the level of brain cells, is the result of self-sustaining patterns of neural activity — a group of neurons starts firing when the initial information is presented and maintains that firing internally when the stimulus is no longer present until the animal acts on that information. Researchers made this conclusion based on years of work painstakingly recording the activity of one neuron or a few neurons in a single local area of the brain at a time. However, neural activity patterns associated with working memory are distributed across many brain regions. Now, recent advances allow scientists to record from many hundreds of neurons at once from several parts of the brain of behaving animals. In addition, brain ‘connectomics’ provides quantitative information about how different brain regions are connected. We will form a collaborative team with four laboratories to take advantage of these new tools and rich data to create anatomically realistic computational models of large brain networks that underlie working memory. We will develop these models based on experimental data collected in mice and monkeys performing delayed response tasks. In one task, for example, a mouse will be exposed to two different somatosensory stimuli, then learn a rule that tells them which of two spouts to lick based on each stimulus. We can study how the brain maintains that information in working memory by analyzing brain activity during the delay between the stimulus and the resulting action. Brain recording technology such as the new Neuropixels probe will allow us to make an unprecedented ‘neural activity map’ highlighting how different brain regions behave during the task. We can then develop computer and mathematical models based on this map, revealing how multiple regions of the brain work together to sustain working memory. Progress in this research project has the potential to provide insights into large-scale circuit mechanisms of cognitive deficits associated with schizophrenia and other mental disorders.
Individuals vary widely in the types of behavioral transitions they undergo in response to adverse environmental conditions. While some individuals respond to adversity by developing persistent negative behavioral states such as hopelessness or anxiety, others are more resilient. Individual differences in neural dynamics likely underlie the likelihood of these transitions, yet we lack a unified framework to detect and quantify them. This is a challenging problem, since networks that encode these transitions are broadly distributed throughout the brain, and changes may unfold across long periods of time. Using a principled theoretical approach (Rajan lab), combined with neural recording performed at multiple temporal and spatial scales (Falkner and Witten labs), we hope to identify multi-region circuit motifs that predict susceptibility and resilience, and to detect when changes in these networks bias individuals toward specific behavioral states.
Learning a complex motor skill like playing tennis or a music instrument requires changes in connections between many neurons in the brain. We understand a great deal about how pairs of neurons alter their connections, but how multiple brain areas collaborate to guide learning across networks of neurons is far less clear. While we’re learning a new motor skill, our sensory system observes how we are doing, and these signals must interact with learning mechanisms in the motor systems that control our actions. What target is the brain using to drive learning computations across multiple brain areas? How does sensory feedback propagate through the brain and guide changes in a subset of neural connections? Our goal is to uncover computational principles of learning motor behaviors. We take an approach that pairs computational tools from artificial neural networks (ANNs) with brain-machine interface (BMI) experiments where the activity from motor areas directly controls the movements of a computer cursor.
ANNs provide powerful ways to explore how large networks perform computations, but drawing parallels between how ANNs and brains learn is challenging because we cannot match neurons in the artificial network to neurons in the brain. BMIs simplify this challenge because they let us experimentally define the ‘behavioral output layer’ of the brain. We will analyze the activity of neurons as animals learn to control a BMI and compare the observed dynamics to those of ANNs to better understand the objectives (targets) that drive learning. This will generate new ways to identify the computations underlying changes within a large group of neurons during learning. We will also perform experiments where we alter the BMI to introduce errors while we record the activity of multiple cortical areas controlling the cursor and the eyes. We will study how visual feedback of errors propagates through the network to change activity in the neurons controlling the BMI cursor and explore whether eye movements that occur as a person gathers visual information contribute to learning. This will allow us to test hypotheses about how feedback drives learning in a network of neurons.