Mathematical Impressions
How do you turn a rubber band into a knot? What happens when you slice a Menger Sponge on a diagonal plane? What is the math behind juggling? In this video series, George Hart illuminates mathematical concepts and surprising hidden geometries that may be found in the world around us.
November 14, 2014
Mathematical Impressions: Curved and Straight?
By George Hart

March 27, 2015
Mathematical Impressions: The Golden Ratio
By George Hart

September 16, 2014
Mathematical Impressions: Long Sword Dancing
By George Hart

May 23, 2014
Mathematical Impressions: Spontaneous Stratification
By George Hart

March 20, 2014
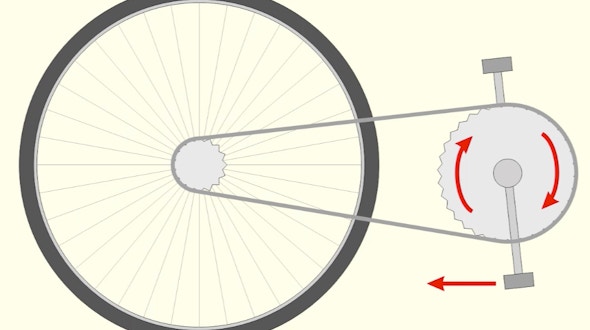
Mathematical Impressions: The Bicycle Pulling Puzzle
By George Hart
February 03, 2014
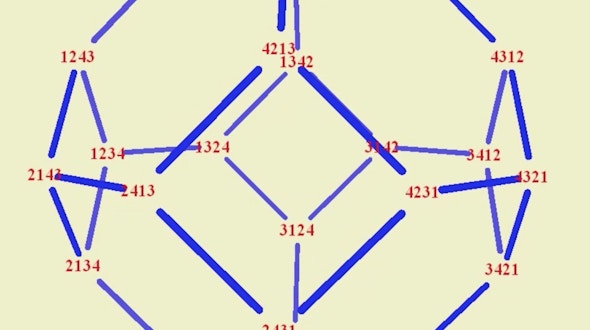
Mathematical Impressions: Change Ringing
By George Hart
October 07, 2013
Mathematical Impressions: Art Imitates Math
By George Hart

August 12, 2013
Mathematical Impressions: Making Music With a Möbius Strip
By George Hart
June 18, 2013
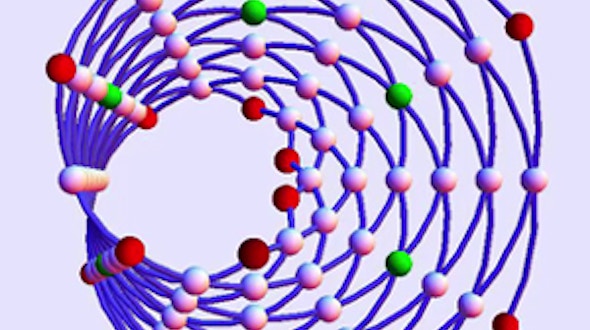
Mathematical Impressions: Goldberg Polyhedra
By George Hart

May 09, 2013
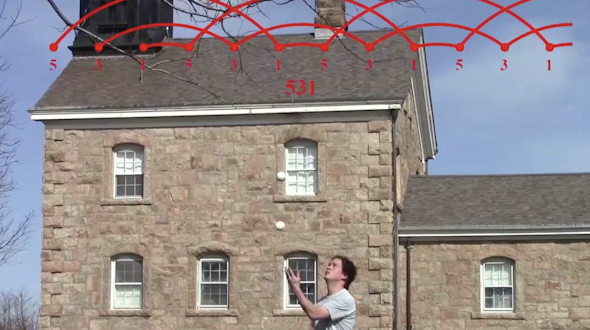
Mathematical Impressions: The Mathematics of Juggling
By George Hart
April 16, 2013
Mathematical Impressions: Bicycle Tracks
By George Hart
March 15, 2013
Mathematical Impressions: Symmetric Structures
By George Hart

- Previous Page
- Viewing
- Next Page