Hitting a Nerve

Of all the high-tech machines used in modern medicine, none sounds more like science fiction than a magnetic resonance imaging scanner. This device, more commonly known as an MRI scanner, uses powerful magnetic fields to turn a patient’s body into a virtual radio antenna. Because every cubic millimeter of the body broadcasts its own set of frequencies, depending on how much water is there and how strong a magnetic field it is exposed to, this scanner is able to “tune in” to these signals and use this information to create images that doctors use to diagnose strokes, tumors, or other illnesses.

hitting-nerve — *Figure 1.* In DTI, a scanner captures an image of the diffusion of water in each small region (voxel) of the brain. The resulting “diffusion tensors” can be portrayed as ellipsoids, which are color-coded according to the direction of strongest diffusion. In the lower left image, for instance, the corpus callosum (the portion of the brain joining the right and left hemispheres) appears clearly in red, indicating that all the nerve fibers there are going in roughly the same direction. The images here are produced by a more advanced DTI technique called HARDI, which allows voxels to contain more complicated shapes than ellipsoids (see inset, upper right). [Image source: “Diffusion Imaging, White Matter, and Psychopathology.” Used with the permission of Paul M. Thompson.]

Yet as futuristic as that sounds, that’s all old technology, dating from the 1970s. The latest versions of MRI are doing much more. Instead of just mapping the functional areas of the brain, doctors can now trace the connections between different parts, creating the equivalent of a “wiring diagram.” These diagrams enable doctors to spot conditions such as Alzheimer’s disease and post-concussion syndrome that are primarily disorders of the brain’s connecting fibers. And they can use these three-dimensional wiring diagrams to plan delicate brain surgeries, lessening the risk of damaging critical fibers.

What made these leaps possible is not so much a new technology, but a smarter way to use the old: a highly mathematical idea called diffusion tensor imaging. David van Essen, a researcher at George Washington University and the lead investigator of the massive Human Connectome Project, says that diffusion tensor imaging is transforming the discipline of brain mapping just as dramatically as satellite imaging and Google Earth transformed our view of our world. “Brain cartography, broadly writ, is one of the great challenges of the twenty-first century,” says van Essen. And according to mathematicians like UCLA’s Paul Thompson, “The advances have mostly been in the mathematics, not in the hardware.”

From MRI to DTI

The great advantage of standard MRI scanning over X-ray imaging is that MRI scans are sensitive not only to the water in your body, but also to to small differences in water content and state. For example, fluids appear brighter than fatty tissue, in which the water is bound tightly to larger protein molecules. Thus, MRI scans can image soft tissue, such as your brain, heart or muscles, and can readily detect tumors, which typically hold extra fluid.

However, traditional MRI scans were essentially useless for imaging the brain’s white matter, where all the connections between neurons are. It wasn’t until the early 1990s that biomedical engineers realized how they could wring much more information out of an MRI scan: an ingenious trick, called diffusion imaging, now lets doctors see not only where the water molecules are, but where they are going.

Water moves around in the body for various reasons. One such reason is diffusion, a process that happens even in stationary fluids and in solid tissue. Diffusion arises from the random jitters, called Brownian Motion, that all molecules undergo. Water molecules will jitter more if they are in a fluid, less if they are bound to a larger molecule (such as a protein) or if in an enclosed space (such as a nerve cell).

The innovation was to hit a water molecule with a magnetic pulse that tips its hydrogen atoms over on their sides, and then a few milliseconds later hit it with a second pulse that tips them back again.

The first key piece of MRI mathematics was discovered more than 150 years before magnetic resonance imaging was invited. It was known as the Fourier Transform.

(See Sidebar, “Fourier Transforms and MRI,” for an explanation of how standard MRI works.) The second pulse should stop the radio signal coming from the hydrogen atoms. However, if the water molecule has moved, the second magnetic pulse will not be the right strength, because, just as in regular MRI, the pulses are shaped in such a way that they are stronger on one side of the body and weaker on the other. This disparity results in a residual radio signal, whose strength is dependent upon the distance the water molecule moved.

In essence, diffusion imaging is both a second layer of magnetic resonance imaging, and a second layer of the Fourier transform. The first layer encodes a molecule’s position, and the raw data lies in the Fourier transform space of position (called k-space in radiology lingo). The second layer encodes a molecule’s displacement over a short time interval, and the raw data lies in the Fourier transform space of displacement (which is called q-space).

The first version of diffusion imaging, called “diffusion-weighted imaging” (DWI), simply measured the total amount of jiggling at every point in the brain. A voxel (see sidebar) would be colored white if the apparent diffusion coefficient was high, black if it was low. Some of the very first DWI scans showed dramatic contrasts between healthy brain tissue and tissue that had been damaged by a stroke. Strokes destroy the integrity of cell walls in the brain, allowing water to diffuse more freely. Therefore a stroke-injured region lights up brightly in a DWI image, but not in a regular MRI scan. It isn’t the amount of water that has changed but the mobility.

But there was still a problem with applying DWI to white matter. In gray matter, the water molecules are equally mobile in all directions. But in white matter, they are not. Water diffuses easily along the long, narrow axons that link neurons together, but it diffuses slowly through the cell walls and especially slowly through the fatty, protein-rich myelin sheath that surrounds many axons. As a result, the apparent diffusion coefficient will look large if the magnetic gradient points along the axon, but small if it points perpendicularly. Obviously, a medical test that does not test what it hopes to test is not very useful.

The source of the problem—and also its solution—lay in the mathematics, not in the machine. Doctors were measuring the diffusion coefficient as a scalar, which could be translated into the brightness of a pixel in a black-and-white image. A scalar can easily be used to geometrically describe a sphere. But in an anisotropic material, atoms diffuse not into spherical blobs, but into ellipsoidal ones. And to describe an ellipsoid, you need more information—the length of its long axis, the length of its shorter axes, and the direction it points. This information can be summed up in a symmetric 3-by-3 matrix called the diffusion tensor.

DWI requires only one measurement in each voxel—mathematically, the trace of the diffusion tensor. But DTI requires six measurements to obtain the full diffusion tensor, because that is the number of independent entries in a symmetric 3-by-3 matrix. In practice, however, neurologists use quite a few more measurements than the minimum. According to Paul Thompson, a typical DTI scan might use 30 different gradient directions; his group at UCLA uses 105. The patient’s tolerance for sitting in a noisy, claustrophobic MRI machine starts to become a significant constraint, because a DTI scan may take as many as 10 to 20 minutes. “There’s a tradeoff between the signal-to-noise ratio and the patient’s irritation,” Thompson says.

The first medical applications of DTI involved a concept called the “fractional anisotropy,” or the ratio between the amount of diffusion in the “easy” direction (along the nerve fibers) and the diffusion in the “hard” directions. Biologists believe that this ratio is a proxy for the structural integrity of axons. A high anisotropy means that your myelin layer is in good shape. When the axons are damaged, as in post-concussion syndrome or Alzheimer’s disease, the fractional anisotropy is reduced. Even in normal brains, fractional anisotropy increases during childhood and adolescence, as our axons develop their myelin sheaths, and then begins to decrease after age 30 (a depressing prospect for 30-somethings).

Though these discoveries were very exciting for biologists, they still did not exploit all of the information available in the diffusion tensor. For a mathematician like Thompson, the most exciting application of DTI is tractography—constructing a “circuit diagram” for the brain.

hitting-nerve3 — *Figure 2*. Diffusion tensor imaging allows doctors to visualize the 3-dimensional “wiring” of the brain in spectacular detail, through a process called fiber tractography. Here, the principal axes of the diffusion ellipsoids (as seen in Figure 1) have been joined to create the visual appearance of fibers. In the middle image, for instance, the red-shaded fibers of the corpus callosum can be clearly seen connecting the two hemispheres of the brain. [Image source: “Diffusion Imaging, White Matter, and Psychopathology.” Used with the permission of Paul M. Thompson.]

In each voxel of a DTI scan, the diffusion tensor encodes both the shape and orientation of the ellipsoid formed by diffusing water molecules. The long axis of the ellipsoid is presumed to be the direction in which most of the axons in that voxel are aligned. If you imagine joining up the ellipsoids to form a continuous cable, you get a view of the brain that looks very much like a densely wired machine. (See figure.) The “cables” are somewhat misleading, because there are no physical structures in the brain that look like wires. But in spite of this caveat, they do convey accurate anatomical information. For example, you can see a side-to-side highway crossing the corpus callosum, which connects the brain’s hemispheres. You can also see a front-to-back highway joining Broca’s and Wernicke’s areas, used in speech production.

Neurosurgeons jumped on tractography eagerly. Despite being only about 15 years old, the technique “is pretty much used routinely” to plan brain surgery, says Alexandra Golby, a neurosurgeon at Brigham and Women’s Hospital in Cambridge. “Its big strengths are that it can be done preoperatively, it’s not invasive, and you can query large areas simultaneously,” she says. (The other way to avoid cutting important connections is electrical stimulation of different parts of the brain during surgery, which requires the patient to be awake and is very invasive.) Tractography can also show whether a tumor has pushed the nerve fibers aside or infiltrated them—a difference that has significant consequences for later treatment.

In one respect, however, DTI has turned out to be too simplistic. Axons are typically only a few microns in diameter. However, the best images feasible with MRI are many times coarser than this—a voxel in an MRI scan is typically a cube about three millimeters wide—so it is currently impossible to view individual axons with MRI technology. Neurologists are just beginning to experiment with scanners that use stronger magnetic fields, but at best these will improve the resolution by a factor of two. In other words, the voxels will still be thousands of times larger than the axons.

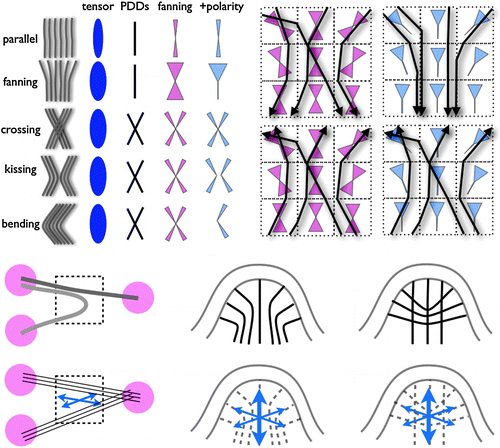
hitting-nerve4 — *Figure 3*. Fiber tractography unfortunately faces many ambiguities. Top left: The ellipsoidal diffusion tensor assumes that all the axons in a given voxel are parallel. However, in many cases they fan out, cross, or “kiss” (come close to one another without crossing). In each case the diffusion tensor (blue ellipse) appears the same. Different assumptions about the small-scale geometry of the axons can lead to very different large-scale models for the “wiring” of the brain, as shown at top right. [Image source: “Tractography: Where Do We Go From Here?” Used with the permission of of Saad Jbabdi.]

This isn’t a problem if almost all of the axons in a voxel are oriented in the same direction. But if two or more nerve fibers cross within a given voxel, the diffusion tensor becomes ambiguous. Likewise, if the nerve fibers fan out, as they do when they reach the cerebral cortex, a diffusion ellipsoid cannot correctly represent the asymmetry between the narrow end and the wide end of the fan. The heart of the problem is once again mathematical. The diffusion tensor is only a mathematical model—one that works well for simple anisotropic materials, but not so well for something as complicated as the human brain.

The most principled solution, called diffusion spectrum imaging (DSI), is to compute a realistic “orientation distribution function” (not just an ellipsoidal diffusion surface) for the axons in any voxel. But this requires much more raw data. Six data points per voxel are enough to compute a diffusion tensor. But six points are a really tiny sample of q-space In practice, about 500 measurements seem to be enough to significantly improve the visualization of crossing and fanning fibers. But if patients are already unwilling to sit still for 10 minutes for a DTI scan, imagine how they would feel about a DSI scan that takes five times longer! For that reason, several research groups are working hard to figure out how to sample q-space in a more efficient way.

In the meantime, DTI is still a work in progress for visualizing small-scale structures. But it is also providing important insights into the larger-scale architecture of the brain. Paul Thompson recently joined ten other neurologists and imaging experts on a study of people with a version of the clusterin gene that has been shown to be associated with Alzheimer’s disease. People with the “bad” version of the gene had, on average, reduced amounts of fractional anisotropy even in their early twenties—half a century before they started showing symptoms of Alzheimer’s. With the help of such research, doctors may one day be able to identify Alzheimer’s patients early enough stave off their symptoms indefinitely.

But to Thompson, even the results on Alzheimer’s disease are just the beginning. “On the horizon, I think we may find that many disorders arise from aberrant connectivity,” he says. “There are many mental disorders whose causes we don’t know yet. I hope that we can transfer some of these from the psychiatry bucket to the neurology bucket. I believe that isn’t too far-fetched a prospect.”

▀ ▀ ▀

Sidebar: Fourier Transforms and MRI

The first key piece of MRI mathematics was discovered more than 150 years before magnetic resonance imaging was invented. It is known as the Fourier transform.

As early as the 1950s, physicists had understood the principal of nuclear magnetic resonance. When you put a sample—a crystal, or a human body—inside a uniform magnetic field, the protons will all start spinning in parallel, like tops. When you tip a spinning top to the side, its axis of rotation will slowly turn in a circle, or precess. A similar phenomenon happens when you tip the protons with a radio wave. The rotating axis causes the protons to emit a radio signal whose frequency is related in a simple way to the strength of the magnetic field.

So far this was just an observed physical phenomenon. But in 1971, a physicist named Paul Lauterbur discovered how to use magnetic resonance to make an image. If you apply a magnetic field that is not constant but has a gradient from top to bottom, or left to right, or front to back, you can give each region (or voxel, the three-dimensional equivalent of a pixel) inside the body its own unique set of magnetic fields; say, 4.5 tesla up, then 4.2 tesla toward the front, then 4.7 tesla toward the right. If your radio antenna picks up the three frequencies corresponding to those three magnetic field strengths, you know exactly where that signal came from. You can thus “listen in” on the hydrogen atoms in any location in the body. Lauterbur won the 2003 Nobel Prize for his discovery.

Of course, the body doesn’t have hydrogen atoms in just one location. Rather, every water molecule in the body has two hydrogen atoms. So in reality, your MRI scan will be a very complex mixture of frequencies coming from different locations in the body. Mathematically, the raw MRI data is the three-dimensional Fourier transform of the density of water molecules in the body. A simple Fourier inversion turns the raw data into a beautiful black-and-white picture, where the brightness of any voxel conveys how much water there is in that cubic millimeter of the body.