Duck Versus Catch: How the Brain Rapidly Responds to Context

If you’re in the middle of a baseball game and see a ball or hot dog hurtling toward you, you’ll probably try to catch it. But if you’re rock climbing or walking down the street, a flying object might make you duck or jump out of the way. How does the brain know how to respond to the same visual cue in completely different ways? More specifically, how do our neural circuits use context to compute the most appropriate behavior?

“Context changes in the environment all the time,” says Mark Stokes, a neuroscientist at the University of Oxford in the United Kingdom. “We simply don’t know how the brain processes information differently according to different contexts.”

What neuroscientists do know is that the brain makes these adaptive decisions quickly — faster than it takes to alter the structure of neural circuits. “So something about the dynamics of the neural circuit must change,” says David Sussillo, a research scientist at Google and an investigator with the Simons Collaboration on the Global Brain (SCGB).

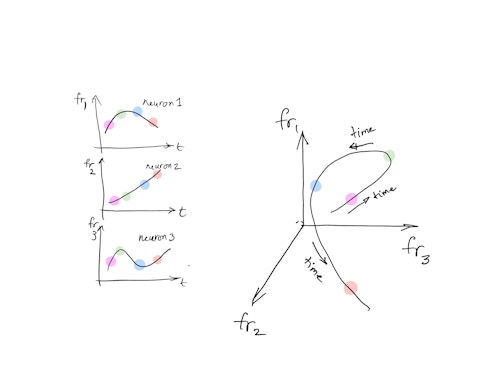
Mehrdad Jazayeri, a neuroscientist at the Massachusetts Institute of Technology and an SCGB investigator, and his collaborators are exploring this notion by analyzing how the state of a group of neurons — a description of the activity of all the individual cells in high-dimensional space, where each axis in the space represents the neural activity of one neuron — shifts with context. The researchers found that the brain represents different contexts by confining neural activity to parallel landscapes within the broader space. “The idea is that the brain will respond differently depending on where it is in state space,” says Stokes, who was not involved in the study. “It’s exciting both conceptually and methodologically.”

Jazayeri’s team is studying context by examining how animals encode time. Musicians in an orchestra, for example, can play a piece of music quickly or slowly, depending on the whims of the conductor. “The brain is highly flexible when it comes to timing,” Jazayeri says.

In a previous study, the researchers trained monkeys to reproduce a specific time interval by moving their eyes to a target after the desired time had elapsed. They found that the brain produces a distinct pattern of neural activity during the task. To reproduce the desired interval, the animals altered the speed at which that pattern unfolded. “For a longer interval, it takes longer for the pattern to evolve,” Jazayeri says. “For a shorter interval, the brain generates the same trajectory but reaches the endpoint faster.”

In the new study, the researchers wanted to figure out whether the same principle — controlling the speed at which neural activity evolves — underlies more complex forms of mental calculation. They trained monkeys to perform a sophisticated version of a task known as ‘ready, set, go.’ Animals were shown two flashes of light separated by a specific time interval. Depending on a color-coded cue, they had to reproduce the time delay or produce a delay that was 50 percent longer. The time-delay cues — factors of 1 or 1.5 — represent different contexts. To complete the task, the animal had to have two levels of flexibility: It had to remember the time interval and know whether to reproduce it exactly or make it 50 percent longer.

Researchers recorded the activity of 100 to 200 neurons in part of the dorsal medial frontal cortex as animals performed the task. The scientists then tracked individual neurons’ activity in high-dimensional space over time, defining a trajectory of activity. Analyzing such neural trajectories is particularly challenging because both their speed and position change over time. Most research solves this problem by reducing the dimensions of the data to 3-D subspaces that are easy to visualize. “In that case, we’re on solid intuitive ground because we can visualize trajectories,” Sussillo says. “What Mehrdad’s group realized is that we have to move beyond that.”

Jazayeri’s team developed a new method, dubbed KiNeT (kinematic analysis of neural trajectories), to analyze the geometry of population activity in high dimensions. KiNet can compare two trajectories in state space, both in terms of where they are and how fast they go. “A manifold in 8-dimensional space is completely unintuitive,” Jazayeri says. “Our analysis was built around the idea that neural trajectories might do weird stuff in high dimensions, and we won’t guess it, so the analysis has to do it for us.”

“The only scientifically valid way to analyze these things is not by finding a projection that fits the hypothesis but to formalize the geometry in the native space,” Stokes says. “They have a clever way to reduce the data to its most relevant high-dimensional space, to track position, velocity, angle, all those geometric properties. That’s quite novel and will be useful for future research.”

KiNet analysis reveals that these trajectories aren’t a random tangle but lie within a specific structure, or manifold. Deciphering the geometry of that structure is important because it indicates how constrained the trajectory is, which in turn is a measure of the underlying neural circuitry, Jazayeri says. “Learning a task constrains what neurons can do.” (The structure is defined as an animal learns a task — once mastered, neural activity is constrained within that structure.)

To better understand the constraints embedded in these trajectories, the researchers approached them as a dynamical system. Dynamical systems are special because they evolve according to some specified trajectory that depends on the system’s initial conditions and its inputs. The trajectory of a pendulum, for example, is fully determined by where it starts and the initial push. “The laws of gravity explain how a pendulum works,” Jazayeri says. “The question is, what laws does the brain uses to control patterns of activity?”

Dynamical systems can be described by three basic factors: the interaction between state variables (the parameters that define the system), the system’s initial state and external inputs to the system. If you imagine neural trajectories as a marble moving along a track, the track represents a manifold within state space. Starting the marble at a steeper part of the track is equivalent to changing the initial conditions, and giving the marble a push is the equivalent of changing the input. Jazayeri’s team asked whether the behavioral flexibility they observed, and the underlying shifts in neural trajectories, could be explained by changes to the system’s input or the initial conditions.

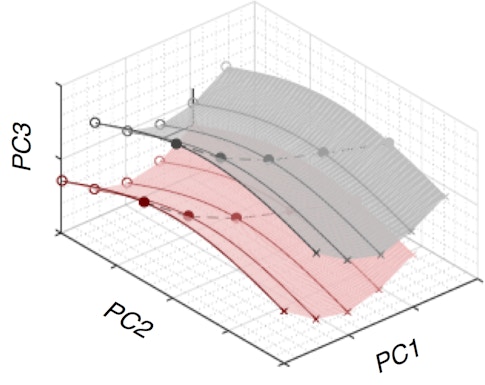
Analyzing the geometry of neural trajectories, researchers found that animals encoded the two variables in the task — the gain (1- or 1.5-fold the duration) and the duration of the interval itself — in two different ways. Gain information was represented in the brain by two similarly shaped manifolds, one representing each condition. When the animal wanted to switch between the two different conditions, its neural activity shifted from one manifold to the other. That shift is driven by input from another part of the brain, the equivalent of giving the marble a push, which reconfigures the behavior of the underlying neural circuit.

The duration of the time interval was represented by the neural trajectory’s starting point on that manifold. This corresponds to a change in the initial conditions, the equivalent of starting the marble on a steeper part of the track.

During a trial with a gain of 1, for example, the animal sees the gain cue and shifts neural activity to the appropriate manifold. The animal then detects the time interval and uses that information to find the right starting point on the manifold. “As the animal measures the interval, it won’t forget the gain because it’s already on right manifold,” Jazayeri says.

Neural networks as model organisms:

To confirm their interpretation, the researchers built a recurrent neural network (RNN). “RNNs are becoming a powerful tool in systems neuroscience because they provide an explicit real mathematical model representing a dynamical system,” Jazayeri says. “They are instantiations of dynamical systems with neurons.”

The approach builds on a study published in 2013 by Sussillo, Valerio Mante, Krishna Shenoy and Bill Newsome, all SCGB investigators. The study was the first to use RNNs as a sort of model organism. Researchers recorded neural activity as monkeys performed a contextual version of the random dot-motion task, in which the animals watching a display had to report the dots’ direction of motion on some trials and the dots’ color on others. To make sense of the complicated data they collected, researchers trained an RNN model to perform an analogous task. Reverse engineering the model revealed that context information drove the system to process each type of information differently, producing the correct solution. The RNN data resembled the animals’ neural activity, suggesting that the prefrontal cortex uses the same approach.

In the new study, Jazayeri’s team trained two types of RNNs to perform the same task as the monkeys, replicating the animals’ output. One RNN incorporated both input and initial conditions into the model and one used only the latter. “Then we opened up the RNNs and analyzed them using the same tricks we use to analyze the brain,” Jazayeri says. “The one that looked similar to the brain had both inputs and initial conditions controlling the two factors.”

“RNNs allow them to make more formal predictions of what you’d expect in a dynamical system,” Stokes says. “It is not a formal proof by hypothesis but allows you to play around with parameters and see what happens.”

In a review of the paper in Neuron, Sussillo outlines suggestions for using RNNs in neuroscience more effectively. “RNNs are useful for making hypotheses,” he says. “You can train and optimize and reverse engineer them.” This is especially important as neuroscience becomes more complex and researchers need to create models capable of performing more sophisticated tasks. Sussillo cautions that it’s important to train RNNs with a wide range of hyperparameters so that the network doesn’t generate a ‘boutique’ solution that works only under a narrow set of conditions. “If you don’t train with a wide range of hyperparameters, you might find a solution that is just so for the particular hyperparameters you picked,” Sussillo says.

Shifting manifolds:

Jazayeri notes that it makes sense to encode gain and interval information separately. Good tennis players, for example, don’t need to relearn the game when moving from a grass to a clay court because they can use existing skills, merely shifting their neural activity to account for a slower bounce. He speculates that this type of hierarchical approach — having structures that are similar but generalizable to different contexts — helps in learning.

The implications go beyond simple timing and may apply to the broader question of how cognitive flexibility comes about: “Our best guess for rapidly switching what the brain can do comes from switching the initial conditions or switching the input,” Jazayeri says. “When instructions are implicit, for example, coming from an internal memory, then the brain represents that information as an initial condition of the system. When instruction is provided explicitly, it’s represented as input.”

The study demonstrates how new input to the system — in this case, context — reconfigures the underlying neural circuits, enabling the same group of neurons to perform related computations by simply shifting their dynamics. Sussillo dubbed this idea computation-through-dynamics. He and Jazayeri, along with Mante, Shenoy and Maneesh Sahani, are further exploring this idea in their ongoing SCGB project.

“Being in different parts of the landscape means you have different computations available, so you don’t have to change the underlying network structure to do these different computations,” Stokes says. “You just rely on the dynamics of the system to find new parts of the landscape to do computations.”

The fact that the two contexts in the experiment are represented in the brain by two parallel manifolds suggests a functional separation between what happens in each one. “Both landscapes are geometrically similar but occupy a unique part of state-space,” Stokes says.  “The answer to context 1 does not interfere with processing the answer to context 2.” That’s potentially important not just for correctly interpreting the context, but also because it might generalize to other computations, Stokes says. “You have separable units that can be used as functional components in other tasks,” he says, though he notes that Jazayeri’s team didn’t study this explicitly. “An indirect implication from the paper is how to create not just non-overlapping but transferable contexts,” Stokes says. “Context-dependent processing allows for protection from interference but also, though they haven’t yet shown how, allows you to package these kinds of computations to other contexts if that becomes helpful.”

That may have implications for improving artificial intelligence (AI). “A big problem in AI is how to train networks in a context-dependent manner so that they don’t just overwrite old learning,” Stokes says. “You want to have modules of sub-tasks that can work together and don’t interfere with each other.”

Google’s DeepMind division has developed deep-learning algorithms capable of playing complex Atari games, for example. But those programs have a hard time with certain tasks. “They can’t learn two Atari games simultaneously without interference,” Stokes says. Instead, “it treats the two games as one giant mega-task.” If the algorithm could understand context the way the brain does, it could learn one game in one context and a second game in another, toggling between them without interference.