Old Problems, New Tools: Adapting Applied Mathematics for Quantum Physics

Flatiron applied mathematician Jason Kaye is bringing powerful new approaches to quantum physicists to help them answer big questions about small particles.

Jason Kaye is an associate research scientist at the Flatiron Institute.

Physicists have spent a long time understanding the mechanics of the world we live in, from how rivers move to how galaxies form. Over the years, they’ve come up with many highly successful models that can describe the behavior of these and other systems. Yet an understanding of the movements of the tiny particles in the universe — electrons, photons and so on — is often still elusive. The small scale of the quantum world, with its bizarre and indecisive behaviors, makes modeling next to impossible. To make sense of the quantum realm, physicists need new strategies.

That’s where Jason Kaye steps in. An applied mathematician at the Flatiron Institute, Kaye works with physicists to help solve tough quantum-specific problems with the aid of applied mathematics and scientific computing. By translating the quantum realm into the language of mathematics, Kaye can use complex algorithms to understand systems that couldn’t otherwise be modeled.

Kaye is a joint member of the Flatiron Institute’s Center for Computational Mathematics (CCM) and its Center for Computational Quantum Physics (CCQ). Prior to joining the Flatiron Institute, Kaye earned a doctorate in mathematics from New York University, a master’s in mathematics from the University of Cambridge, and a bachelor’s in applied mathematics from Brown University.

How can applied mathematics be useful for quantum physics?

Much of applied mathematics has focused on enabling simulations of phenomena in classical physics, from electromagnetics to fluid dynamics, and it has been very successful at pushing these fields forward. Applied mathematicians have developed a variety of tools and techniques that allow them to simplify complex systems by ‘cutting corners,’ without losing essential information. We are able to do this by looking for hidden structure in the equations describing these systems and making careful, controlled approximations based on these structures.

Many techniques developed in the applied math community in the context of classical physics have not quite made their way into the quantum physics community. There’s a significant language barrier between applied mathematicians and quantum physicists. I’m working to translate between them, so that lessons we’ve learned in the past few decades can be applied to quantum problems.

What kinds of quantum systems can you model?

Quantum physicists want to understand and simulate small-scale systems, like the electrons in the collections of atoms comprising molecules and materials. The interactions between electrons tell you about small-scale phenomena like chemical bonding and large-scale properties like the conductivity of a material.

Physicists try to model these structures, but it’s very difficult, even for simple systems. In the classical physics picture of particles — the old picture — every particle is essentially described by six numbers: its coordinates in space, x, y and z, and its velocities in these three directions. With just six numbers per particle, you are able to describe large numbers of interacting classical particles. The quantum physics picture — which is required to correctly model the behavior of real, small-scale physical particles like electrons — is much more complicated. In the quantum picture, particles don’t have well-defined positions or velocities, so instead we have equations describing, more or less, the probabilities of particles having certain positions, or velocities, or other physically observable properties. When you look at a system with multiple particles, you must consider the probabilities of every combination of possible particle positions or velocities. This means the amount of information you need to keep track of grows exponentially with the number of particles.

The concept of self-energy describes how a particle embedded in a quantum system influences its own motion at a later time: the particle "pushes" on the larger system at time t', and as a result the system pushes back on it at a later time t. This plot shows the self-energy of an electron for a simple model of an atomic lattice in an electric field. Using a method called "hierarchical off-diagonal low rank compression," the self-energy can be divided into square blocks, and the information in each block compressed (similar to image compression algorithms, like JPEG). The black dots correspond to the number of bits of data required to represent a block to a given accuracy. As the size of the blocks grows, the number of bits increases only very slowly, indicating that the interaction between distant moments in time is highly compressible. In this situation, the full self-energy can be captured on very large time frames using few bits of data, providing a path towards long-time simulations of quantum physics. Reference: J. Kaye, D. Golež, *SciPost Phys*.10 (2021) 91.

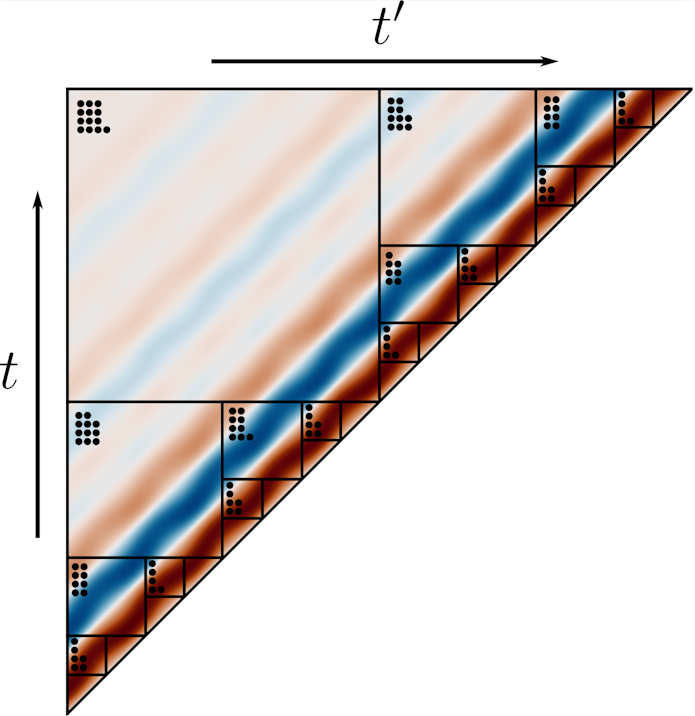
So we need to find a way to make approximations and simplifications. Physicists are experts at certain types of approximations, and applied mathematicians offer another perspective, which in some cases allows you to go even further. This leads to new strategies to compress the number of bits required to describe quantum systems, by systematically identifying and eliminating redundant information, or by describing the components of the equations efficiently.

We have accumulated a large bag of tricks developed in the context of classical physics, and it turns out that many of these tricks are also useful in the quantum world.

Let me give a concrete example. It is known that shining a laser on certain materials can induce a phase transition — such as a transition between a metal and an insulator — which could be a path toward active control of material properties and could lead to a variety of possible technological applications. We can understand this phenomenon using atomic-scale simulations. To avoid paying the large cost of simulating many atoms in the material at once, physicists have designed clever methods of zooming in on a single atom, or a small subsystem, in full detail, and making a simpler approximation for the rest.

However, the price you pay for this approximation is what we call a full memory dependence; to move the atom forward in time one step, you need to look over the whole history of the atom’s motion, which is computationally expensive. This is a familiar problem to applied mathematicians; we can compress the history by observing that it contributes in a simpler way to the motion at the current time the farther back you go. So, by combining these approximation methods from physics with compression methods from applied mathematics, we can simulate these types of systems for much longer timescales than with previous methods.

How do you collaborate with quantum physicists?

When I started this work in graduate school, I felt there was a language barrier that was preventing many applied mathematicians from working on interesting problems in quantum physics. I started talking to as many people on the physics side as I could, spending time figuring out how to translate quantum physics problems into terms more familiar in applied mathematics. Through this process, I saw that many existing tools and ideas could be helpful, but were not being utilized.

Today, I act as a kind of consultant connecting the CCM and CCQ. I have continued my conversations with physicists, and we continue to find opportunities for transfer of knowledge. We have also found new classes of problems of interest to applied mathematicians, which had not been written down in their language before.

Going forward, we will need to face more and more complex systems for which the exponential scaling of quantum physics must be dealt with. We will see how far applied mathematical ideas can go in making a dent in the exponential barrier, or in revealing that certain problems which seem exponentially hard have a hidden structure or compressibility. There will be many opportunities for collaboration going forward, and I expect the exchange between these fields to continue to grow.