Searching for Shapes in Neural Activity

The parable of the blind men and the elephant tells the story of a group of blind men who encounter an elephant for the first time. Each individual feels a different part of the animal and describes it to the others. Ultimately, each individual’s notion of an ‘elephant’ is an amalgam of the idiosyncratic experiences of all the individuals. Modern neuroscience faces a similar challenge. The neural activity underlying behavior is enormously complex. New technologies that record from many neurons as animals perform complex tasks offer researchers an unprecedented view of that complexity. But like the blind men feeling the elephant, they need a way to make sense of it — to decipher the equivalent of a trunk or a foot and, ideally, to piece those parts together into a cohesive whole.

New methods for analyzing the structure of neural activity — namely, its geometry and topology — offer a way to sift through that complexity. “It’s the next frontier of thinking about neural computations and coding in high-dimensional neural populations,’’ says SueYeon Chung, a project leader at the Flatiron Institute’s Center for Computational Neuroscience who has written numerous papers on geometric representations in neural responses. “Even in brain regions that were traditionally hard to characterize, when you look at the high-dimensional geometry of neural activity, there is structure. And often those structures persist between animals or different tasks, uncovering commonalities and differences. I think that’s why it’s so exciting.”

Two new papers highlight the potential of this approach, using novel analysis methods to reveal geometric forms that give insight into how neural circuits compute. Their respective insights illustrate both the power and future challenges of these approaches, as well as the spectrum — from simple and elegant to complex and powerful — of the functional capacities of different neural circuits. Though these efforts offer glimpses of some of the brain’s more ‘complex elephants,’ they are just a start. Researchers still need to develop new tools for analyzing more complex forms and to synthesize the disjointed insights that emerge. How complete a picture they will ultimately be able to construct remains an open question.

Simple elephants

A logical first step is to focus on ‘simple elephants’: neural circuits that encode information in a sufficiently complex way to not be trivial but are simple enough to yield an understandable insight. In 2019, Ila Fiete, a theoretical neuroscientist at the Massachusetts Institute of Technology and an investigator with the Simons Collaboration on the Global Brain (SCGB), illustrated the simple yet elegant way in which information is encoded in the head direction cells of the thalamus. Fiete and collaborators used a novel analysis approach to show that the head direction network represents this one variable as simply as possible; the collection of neural activity states of this circuit — known as a manifold — is confined to a one-dimensional ring such that position along the ring corresponds to the head direction.

Such a finding begs the question of whether other ‘simple elephant’ circuits exist. In a new study published in Nature, Edvard and May-Britt Moser and collaborators use massive parallel neural recordings to illustrate that the long revered ‘grid cell’ system is such a circuit.

The Mosers discovered grid cells in 2005, an achievement that garnered them a Nobel Prize in physiology or medicine in 2014. These unique cells, found in the medial entorhinal cortex, fire at regular intervals when an animal navigates through space, forming a gridlike pattern of neural activity when superimposed on the physical world. Many researchers went on to theorize that this brain region encodes the animal’s position with a coordinate system uniquely matched to the repeating nature of these cells’ activity. Work by several researchers, including Fiete, all but confirmed this theory, using a combination of existing data, conventional analyses and mathematical theory to paint a picture of how the circuit operates. But directly verifying many of their predictions was impossible without simultaneously recording from many cells. “Grid cells are super sparse,” says Fiete. “If you stick in a conventional probe, if you’re lucky, you’ll record from a handful of cells.” But fully visualizing the network’s encoding scheme would require recordings from 40 to 60 cells, Fiete predicted.

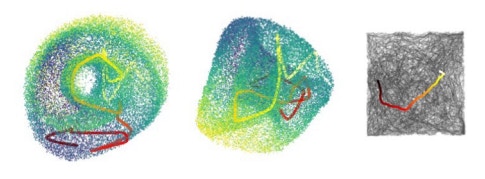
To overcome this limitation, the Mosers’ team recorded from hundreds of grid cells simultaneously using Neuropixels probes — a feat only possible with such a high-density recording electrode — while rats moved freely in an open space. They used two related approaches to analyze neural data, both of which seek to make statements about the nature of the neural manifold defined by the observed neural activity. The first class characterizes the neural manifold’s geometry: its general nature as well as the details of the shape formed when neural responses are plotted graphically.

Using a standard but, importantly, nonlinear method for reducing many neural responses over many observations in time to a smaller set of coordinates, the authors found that the grid cells’ responses took the shape of a torus, or hollow doughnut.

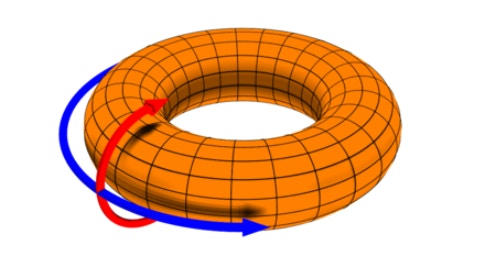
Just as a ring was the simplest possible coding scheme for representing a periodic, one-dimensional variable like head direction, a torus is the natural shape for representing two periodic variables. In the simplest scenario, the repeating grid cell activity of one dimension of space is encoded along one of the torus’s rings, while the activity along the other dimension of space is encoded along the other. Nonlinear methods were critical to obtaining this insight because of the unique, non-flat geometry the researchers discovered.

Geometric analysis can offer particular insights, and in some cases, such as with grid cells, even provide insights that can be displayed visually. However, geometric analyses do not easily lend themselves to precise quantitative statements, nor do they allow easy comparison of multiple manifolds derived from different experiments or different animals. To overcome these limitations, the researchers turned to the second class of analysis, which focuses on the topology of the neural manifold. Topological analysis seeks not to characterize the shape of a manifold but rather to offer an abstract summary of its properties, such as the number and variety of holes and cavities it possesses.

While geometric analysis offers a richer description of a neural manifold with the potential for visualization, the simpler and more abstract description afforded by topological analysis provides a compact, although piecemeal, description more amenable to comparison. “If you want to find common features in highly variable representations, topological data analysis is much better than geometrical approaches, because sometimes you want to ignore low-level details that may survive in Euclidean comparisons,” says Chung.

For example, a topological characterization of the torus manifold would document the presence of two rings — one that’s visible when the doughnut is viewed from above, and one that can be seen when you travel along the edge of the doughnut, moving in and out of the doughnut’s center — and also the presence of a closed cavity that can be seen as you move along the central axis within the middle of the doughnut. When the researchers applied this method to grid cell data, they found the topological signatures of the torus they had initially identified visually. They were able to quantitatively confirm these features in multiple grid cell recordings, suggesting that it is a robust feature of this brain circuit. Moreover, torus features were present in neural activity recorded from sleeping animals, suggesting that the internal connectivity of the grid cell network alone defines the neural manifold its activity resides on.

These results confirm long-standing hypotheses and provide insight into how this brain region encodes space in a way that remains constant regardless of where the animal is located and what it’s doing. Although Fiete and others long predicted that a torus would emerge from these types of recordings, the Mosers’ work illuminates the theory in stunning detail: “To show it visually is very powerful,” says Fiete.

An especially noteworthy feature of this finding was that such a simple geometry emerged even though the animals were engaged in a fairly complex behavior that included unconstrained navigation in a complex environment. As behaviors become more complex, many investigators find that neural representations become more complex, making the Mosers’ discovery in some ways surprising and generally very satisfying. “The beauty of systems like the grid cell system is that they retain their simplicity despite behavioral complexity,” says Fiete.

Piecing together complex elephants

Unfortunately, the tantalizingly simplistic yet nontrivial geometry of the grid cell torus is likely to be rare, especially for neural circuits that are engaged in more complex computations that underlie more complex behaviors. “It’s almost inconceivable that such orderly structures would exist for all the possible behaviors that we can produce,” says Manuel Schottdorf, a postdoctoral researcher at the Princeton Neuroscience Institute.

Research from Schottdorf and his collaborator Edward Nieh, published in Nature in June, illustrates the challenges faced as the brain’s ‘elephants’ become more complex. The study, led by SCGB investigators David Tank and Carlos Brody, applied a similar combination of advanced mathematical analysis and high-density neural recording from animals engaged in navigation. The picture of neural encoding they found during this more complex behavior was far from the neatly bowed torus of the grid cell system, hinting at a more sophisticated functional role for the brain region they studied.

Researchers recorded neural responses from the hippocampus, a key brain region for navigation, as animals navigated through a virtual maze that required them to keep track of visual cues. The researchers used a novel analysis tool called Manifold Inference from Neural Dynamics, or MIND, to uncover the geometric structure of the neural manifold defined by this circuit’s activity. As was the case for grid cells, the researchers found that neural activity was confined to a low-dimensional curved surface. Though the manifold did not have a naturally intuitive geometry like a torus, finding such a relatively low-dimensional structure is helpful because it provides a compact representation of the variables relevant to this behavior. Motion along each direction of the manifold corresponded to changes in each behaviorally relevant variable, such as position or evidence that could be used to guide its decision, much as motion along each ring of the grid cell’s torus encoded a movement direction in space. Importantly, the nonlinear manifold, which is only detectable with nonlinear methods such as MIND, reduced the number of dimensions that were required to robustly predict the responses of other neurons on the manifold to approximately four. Linear methods such as principal components analysis require upward of 40 dimensions.

To solve the navigation task, animals technically only need two variables — their position and their memory of the visual cues that indicate which direction to turn. The researchers found that both of these variables were encoded along the manifold, but so were others, including the animal’s previous choices and its head direction. This additional complexity in representation suggests that the function of the hippocampus is quite different from the grid cell system. “This is a complicated behavior, so perhaps the mouse keeps its options open about variables that might be relevant,” Schottdorf says. “Even though the manifold might represent variables that are not task-relevant, maybe there’s no harm in representing a few more candidate variables that might become relevant later.” Such flexibility and complexity suggests that the hippocampus may be a crucial circuit node in enabling more general behaviors like cognition that may require more intricate coding schemes.

Although the researchers did not study the topology of the hippocampal manifold, their finding that it appears to be approximately four-dimensional suggests that doing so will present unique challenges. Fiete says that for curved manifolds higher than two dimensions, existing methods that identify topological features can offer abstract characterizations of their shape but are a far cry from the pleasing elegance of the grid cells’ torus. The problem is that the shape of higher-dimensional curved manifolds becomes too complex for us to intuit visually — two-dimensional curved manifolds like tori and spheres can be visualized in three-dimensional space, but beyond that, our intuitive sense of shape begins to falter. “Topology is powerful in that it will tell us some things about that manifold — it’ll give us a bunch of characteristics, but then, like the blind men and the elephant, you still have to piece it all together,” she says. The united picture offered by the grid cell network’s topological and geometric descriptions, which satisfyingly relate a two-ring, single-cavity object to the familiar shape of a torus, further highlights how exceptionally rare that discovery may be. For more topologically elaborate manifolds, we may not get that deeper intuitive picture. Theoretical neuroscientists will have to assemble the piecemeal topological description of a manifold to envision an elephant as best we can.

Although understanding higher-dimensional manifolds presents new challenges for theoretical neuroscientists, the task is not hopeless. “We can hope that if there are higher-dimensional manifolds than two-dimensional tori, perhaps they can be decomposed into lower-dimensional structures that are more easily characterized,” says Fiete. Tank and Brody’s work suggests that there is systematic composition within the hippocampal manifold that would naturally lead to this type of decomposition. For example, when researchers added a new variable to the task, the manifold structure increased by one dimension. “That is at least suggestive that there is some sort of constructive mechanism at work” assembling the manifold dimension by dimension, says Schottdorf. Additionally, related work from Tank’s lab has introduced a tantalizing theory that manifolds constructed by other brain regions during this decision-making task do in fact decompose, specifically into two tori, one for each possible decision. In anticipation of future manifolds that are not so forgiving, Fiete is working on developing the tools for identifying how complex manifolds can be broken into simpler parts, with the hope that it will shed light on manifolds much more complex than tori.

In both studies, the fact that neural responses are confined to a manifold, and that they persist without external sensory input for the grid cell manifold, provides strong evidence that these neural circuits are well described as continuous attractor networks. These network models, a cornerstone of theoretical neuroscience, have long been the leading model for how neural circuits perform computations, such as memorizing stimuli, integrating new stimuli with previous information, and using remembered or encoded stimuli to make decisions. But their development has focused largely on their theoretical properties, with only limited experimental evidence. The hallmark of these models, for cases in which a continuous variable like position or direction is encoded, is a low-dimensional space of preferred network states to which all network activity eventually migrates — in other words, a manifold. New analysis tools, such as those developed to study topology and geometry, have finally given neuroscientists the ability to empirically see manifolds in neural activity, indicating that continuous attractor networks are more than theorists’ musings.

Further experimental study is necessary to understand how completely these models capture the properties of real neural activity. For example, whether other neural activity manifolds have the hallmarks of attractor dynamics, and, if so, whether they are as robust to noise as their theoretical attractor model counterparts, remains an open question. “Understanding how these continuous attractors are assembled through development and whether they can be formed through learning is an exciting frontier,” says Fiete.