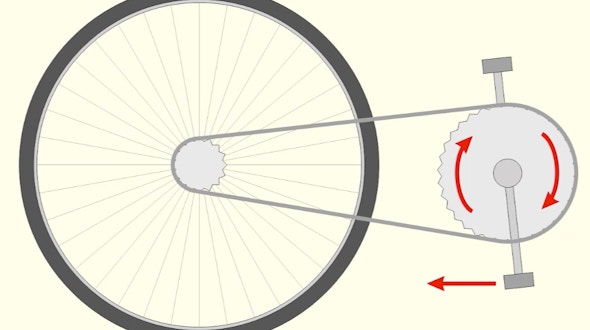
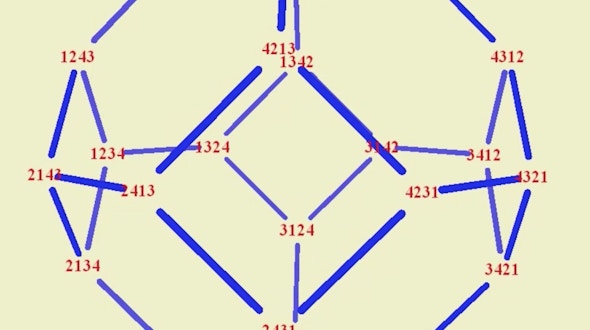
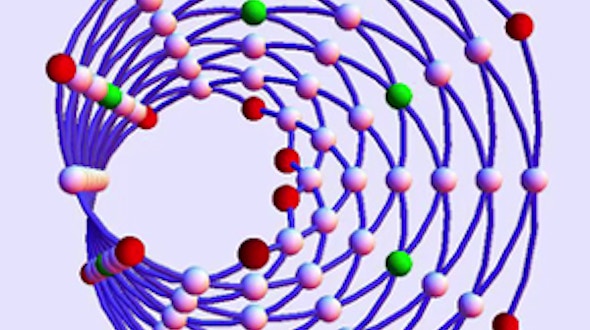
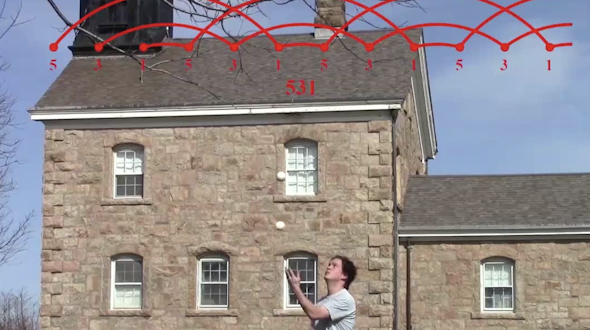
Mathematical Impressions
How do you turn a rubber band into a knot? What happens when you slice a Menger Sponge on a diagonal plane? What is the math behind juggling? In this video series, George Hart illuminates mathematical concepts and surprising hidden geometries that may be found in the world around us.
November 14, 2014
March 27, 2015
September 16, 2014
May 23, 2014
March 20, 2014
February 03, 2014
October 07, 2013
August 12, 2013
June 18, 2013
May 09, 2013
April 16, 2013
March 15, 2013
- Previous Page
- Viewing
- Next Page